Algorithmes gloutons

I. Présentation générale :

Les problèmes algorithmiques sont très variés et certains sont plus compliqués que d'autres.

Prenons par exemple le célèbe "problème du voyageur de commerce". Un commercial débute sa journée dans la ville $A$ et doit passer durant la journée par toutes les villes de $A$ à $D$. On connaît les distances entre chaque ville et le problème est simplement de déterminer la parcours le plus court (en distance ou en temps).

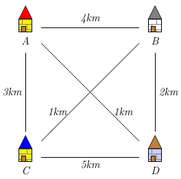
Ce problème est très concret et se retrouve régulièrement dans la vie quotidienne (organiser une tournée de rammassage scolaire, livraison de colis...).

Dans le cas de $3$ villes (en plus de $A$), il est facile d'étudier tous les parcours possibles débutant par $A$ :

1. $A \rightarrow B \rightarrow C \rightarrow D$
2. $A \rightarrow B \rightarrow D \rightarrow C$
3. $A \rightarrow C \rightarrow B \rightarrow D$
4. $A \rightarrow C \rightarrow D \rightarrow B$
5. $A \rightarrow D \rightarrow B \rightarrow C$
6. $A \rightarrow D \rightarrow C \rightarrow B$

Mais s'il y a $10$ villes en plus de $A$ ? Il y a $10\times9\times\dots\times1=10!=362\:8800$ trajets possibles ! Il est dès lors hors de question de tous les étudier.

En termes de complexité, le problème du voyageur de commerce est de complexité factorielle $\mathcal{O}(n!)$.

On doit donc dans bien des cas abandonner l'idée de tester tous les chemins possibles.

Une démarche différentes consiste à :

• en partant de $A$, choisir la ville la plus proche et y aller.
• une fois dans cette ville, choisir la ville non visitée la plus proche et y aller
• recommencer jusqu'à ce que l'on ait visité toutes les villes

C'est la démarche de l'algorihtme glouton, greedy algorithm en anglais : à chaque étape on cherche à maximimiser le bénéfice immédiat sans jamais revenir en arrière.

Cette méthode est rarement exacte : elle ne produit pas obligatoirement la meilleure solution au problème. Mais elle permet bien souvent de proposer une solution satisfaisante en un temps raisonnable.

Ne soyons toutefois pas trop négatif : les méthodes gloutonnes sont très utilisées au quotidien. L'algorithme de Dijkstra qui permet de déterminer le plus court chemin entre deux sommets d'un graphe (et entre deux lieux dans un GPS) repose sur une méthode gloutonne.

Il est facile de la prendre en défaut. Revenons à notre voyageur de commerce dans le cadre de la figure ci-dessous :

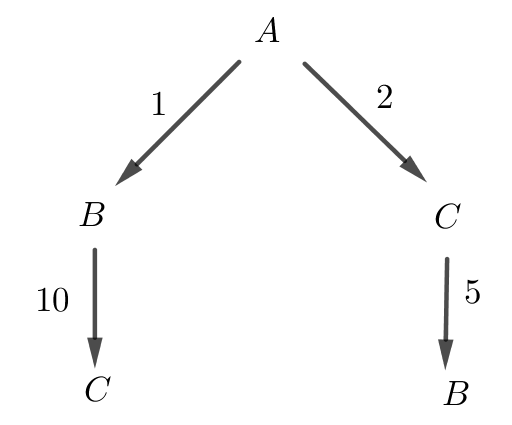
Dans la vie quotidiennes, les trajets $B \rightarrow C$ et $C \rightarrow B$ peuvent être différents (sens interdits, déviations...)

Le trajet le plus court ici est $A \rightarrow C \rightarrow B$ ($7$ km) mais un algorithme glouton choisirait $A \rightarrow B \rightarrow C$ ($11$ km) en cherchant à minimiser la première étape.

II. Premier exemple : La recherche d'un maximum

Imaginons que l'on souhaite déterminer le maximum d'une courbe : on part d'un point quelconque et à chaque étape on se déplace dans le sens de la pente la plus grande. Quand la pente à gauche et à droite est négative, cela signifie que l'on a atteint un maximum.

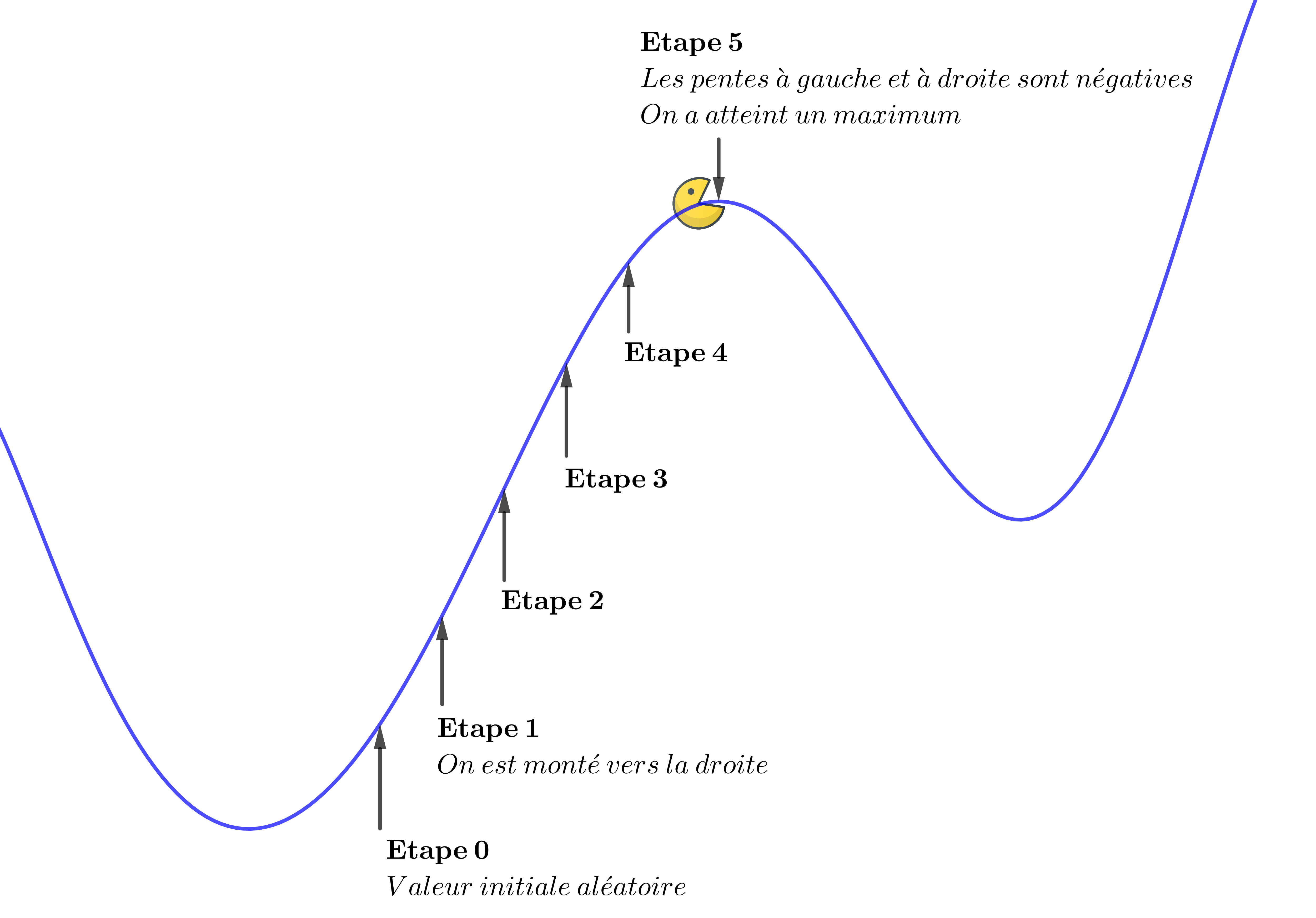
On le voit sur la figure, on n'est pas assuré d'atteindre un maximum absolu. Mais au moins on aura un maximum local.

Codons ce problème : imaginons que l'on souhaite déterminer le maximum de la fonction $f :x \mapsto -x^4+x^3+x^2-x+1$ pour des valeurs de $x$ entre $-1$ et $2$.

pip install numpy

Requirement already satisfied: numpy in c:\programdata\anaconda3\lib\site-packages (1.16.2)
Note: you may need to restart the kernel to use updated packages.

pip install matplotlib

Requirement already satisfied: matplotlib in c:\programdata\anaconda3\lib\site-packages (3.0.3)
Requirement already satisfied: numpy>=1.10.0 in c:\programdata\anaconda3\lib\site-packages (from matplotlib) (1.16.2)
Requirement already satisfied: cycler>=0.10 in c:\programdata\anaconda3\lib\site-packages (from matplotlib) (0.10.0)
Requirement already satisfied: kiwisolver>=1.0.1 in c:\programdata\anaconda3\lib\site-packages (from matplotlib) (1.0.1)
Requirement already satisfied: pyparsing!=2.0.4,!=2.1.2,!=2.1.6,>=2.0.1 in c:\programdata\anaconda3\lib\site-packages (from matplotlib) (2.3.1)
Requirement already satisfied: python-dateutil>=2.1 in c:\programdata\anaconda3\lib\site-packages (from matplotlib) (2.8.0)
Requirement already satisfied: six in c:\programdata\anaconda3\lib\site-packages (from cycler>=0.10->matplotlib) (1.12.0)
Requirement already satisfied: setuptools in c:\programdata\anaconda3\lib\site-packages (from kiwisolver>=1.0.1->matplotlib) (40.8.0)
Note: you may need to restart the kernel to use updated packages.

import numpy as np
import matplotlib.pyplot as plt

def f(x) :
    return -x**4 + x**3 + x**2 - x + 1

abscisses = np.arange(-1, 2, 0.001)

x = abscisses

plt.plot(x, f(x), 'b-')

solution = -(1+np.sqrt(17))/8
plt.plot(solution, f(sol), 'go')

plt.plot(1, f(1), 'ro')

[<matplotlib.lines.Line2D at 0x26a9f977d30>]

Un étude mathématique montre que le maximum est atteint pour $x = -\frac{1+\sqrt{17}}{8} \simeq -0,640388203202$

L'algorithme est la suivant :

• x vaut une valeur donnée par l'utilisateur
• pas vaut une valeur donnée par l'utilisateur
• pente_gauche vaut 1 # on initialise à des valeurs positives
• pente_droite vaut 1
• Tant que max(pente_gauche, pente_droite) > 0 et -1 < x < 2 faire :
  • pente_gauche vaut f(x-pas) - f(x)
  • pente_droite vaut f(x+pas) - f(x)
  • si pente_gauche > pente_droite et pente_gauche > 0 :
    • x prend la valeur x - pas
  • sinon si pente_droite > pente_gauche et pente_droite > 0
    • x prend la valeur x + pas

En python :

def glouton(depart, pas) :
    """
    Cherche le maximum sur [-1, 2] de la fonction f par la méthode gloutonne
    depart est un flottant entre -1 et 2. C'est l'abscisse initiale
    pas est un flottant positif. C'est l'écart entre deux valeurs consécutives
    Renvoie l'abscisse du maximum
    """
    x = depart
    # On initialise les valeurs des pentes afin d'amorcer la boucle
    pente_gauche = 1
    pente_droite = 1
    
    while max(pente_gauche, pente_droite) > 0 and -1 < x < 2 :
        pente_gauche = f(x-pas) - f(x)
        pente_droite = f(x + pas) - f(x)
        if pente_gauche > pente_droite and pente_gauche > 0 :
            x = x - pas
        elif pente_droite > pente_gauche and pente_droite > 0 :
            x = x + pas      
    
    return x

Appliquons cette méthode en partant de $0$ avec un pas de $0,1$ :

glouton(0, 0.1)

-0.6

Et si l'on part de l'autre côté du maximum :

glouton(-0.9, 0.1)

-0.6000000000000001

Peut-on être plus précis ? En diminuant le pas :

glouton(0, 0.01)

-0.6400000000000003

glouton(0, 0.001)

-0.6400000000000005

glouton(0, 0.0001)

-0.6403999999999458

On peut facilement tromper l'algorithme en lui fournissant un point de départ proche de 1 (maximum relatif) :

glouton(0.5, 0.0001)

0.9999999999999449

III. Deuxième exemple : Organiser ses visites

UN problème plus concret cette fois-ci.

Un visiteur passe une journée au parc d'attraction. Il a (parfaitement) prévu sa visite et connait les heures de début et de fin de toutes les attractions l'intéressant dans le parc.

Ces données se présentent ainsi :

Activité n°	$0$	$1$	$2$	$3$	$4$	$5$
Début	$9,5$	$10,5$	$9$	$11,5$	$13$	$11,5$
Fin	$10$	$11$	$12$	$12,5$	$13,5$	$13,5$

Cela signifie que l'activité $0$ débute à 9h30 et s'arrête à 10h.

On a classé les activité dans l'ordre de heure de fin.

La méthode gloutonne consiste à choisir à chaque étape l'activité finissant le plus tôt et dont l'heure de début est supérieure ou égale à celle de fin de l'activité précédente.

On voit bien qu'à chaque étape on choisit le meilleur choix à cet instant sans vue d'ensemble.

Ici on prendrait donc les activités :

• $0$ qui termine à 10h
• $1$ qui termine à 11h
• $3$ qui termine à 12h30
• $4$ qui termine à 13h30

Le pseudo-code :

• activite prend la valeur $0$
• Pour j allant de $0$ à nombre d'activité :
  • Si debut[j] > fin[i] :
    • Affiche j
    • i prend la valeur j

En python :

def activite(debut, fin) :
    nb_activite = len(debut)
    
    i = 0
    print("Activité n°",i , "(Début :", debut[i],"; Fin :", fin[i], ")")
    
    for j in range(nb_activite) :
        if debut[j] >= fin[i] :
            i = j
            print("Activité n°",i, "(Début :", debut[i],"; Fin :", fin[i], ")")

Testons avec les données du dessus :

debut = [9.5, 10.5, 9, 11.5, 13, 11.5]
fin = [10, 11, 12, 12.5, 13.5, 13.5]

activite(debut, fin)

Activité n° 0 (Début : 9.5 ; Fin : 10 )
Activité n° 1 (Début : 10.5 ; Fin : 11 )
Activité n° 3 (Début : 11.5 ; Fin : 12.5 )
Activité n° 4 (Début : 13 ; Fin : 13.5 )

Et avec des données plus grandes :

debut = [0,0,5,6,2,4,8,7,8,8,11,9,13,14,15,18,15,17,19,20,19 ]
fin = [1,5,6,7,7,8,9,10,11,12,14,14,16,18,19,20,20,21,21,22,24]

activite(debut, fin)

Activité n° 0 (Début : 0 ; Fin : 1 )
Activité n° 2 (Début : 5 ; Fin : 6 )
Activité n° 3 (Début : 6 ; Fin : 7 )
Activité n° 6 (Début : 8 ; Fin : 9 )
Activité n° 10 (Début : 11 ; Fin : 14 )
Activité n° 13 (Début : 14 ; Fin : 18 )
Activité n° 15 (Début : 18 ; Fin : 20 )
Activité n° 19 (Début : 20 ; Fin : 22 )