Codage d'entiers positifs

Un ordinateur sauvegarde et manipule toutes les données sous forme de $0$ et de $1$ en binaire.

Mais qu'est-ce que le binaire ?

Comment convertir un nombre entier en binaire ?

Quels nombres peut-on stocker ?

leibniz.gif

Médaille créée par Leibniz pour célébrer sa "découverte" du binaire

yikink-hexa.gif

Page du "Yi Jing", ouvrage du premier millénaire avant notre ère, utilisant déj) le codage binaire

I. La base 10

Au quotidien nous utilisons la base $10$ (sans doute à cause de nos $10$ doigts !).

Dès l'école primaire nous apprenons à parler d'unité, dizaine, centaine, milliers... Par exemple le nombre $1\:084$ compte :

  • $1$ millier
  • $0$ centaine
  • $8$ dizaines
  • $4$ unités

Si l'on se souvient que $10^3=1\:000$, $10^2=100$, $10^1=10$ et $10^0=1$ on peut donc écrire :

$ 1\:084=1\times 10^3 + 0 \times 10^2 + 8 \times 10^1 + 4 \times10^0$

On peut avec cette méthode écrire tous les nombres entiers.

Chaque puissance de $10$ est multipliée par un coefficient entre $0$ et $9$ (car de $0$ à $9$ on a $10$ valeur possibles).

De plus, en utilisant toutes les puissances de $10$ entre $10^0$ et $10^5$ on peut écrire tous les nombres de $0$ (tous les coefficients à $0$) à $999\:999$ (tous les coefficients à $9$) : il y en a $10^6$.

Ainsi fonctionne la base $10$. Pour le binaire on fonctionne de la même façon mais avec des puissances de $2$

Exercice 1 :

Ecrire le développement en base $10$ des nombres suivants :

  • $24$ :
  • $204$ :
  • $10\:000$:

Exercice 2 :

Et si on utilise une autre base ? Pour la base $5$ par exemple on utilise les puissances de $5$ qui sont $1$, $5$, $25$, $125$, $625$... Convertir en base $10$ les nombres suivants écrits en base $5$ (comme l'indique l'indice $5$ à la fin du nombre) :

  • $24_5$ :
  • $204_5$ :
  • $10\:000_5$:

II. La base 2 : le binaire

II.1 Présentation

Pour le binaire, on fonctionne de la même façon mais avec des puissances de $2$. Les seuls coefficients possibles sont alors $0$ et $1$.

C'est la plus petite base possible. En effet les puissances de $0$ et $1$ ne permettent pas de coder beaucoup de nombres...

On rappelle les premières puissances de $2$ :

Exposant $n$ $0$ $1$ $2$ $3$ $4$ $5$ $6$ $7$ $8$ $9$ $10$ $...$
$2^n$ $2^0$ $2^1$ $2^2$ $2^3$ $2^4$ $2^5$ $2^6$ $2^7$ $2^8$ $2^9$ $2^{10}$ $...$
Valeur $1$ $2$ $4$ $8$ $16$ $32$ $64$ $128$ $256$ $512$ $1024$ $...$

Ainsi, le nombre $10_2$, exprimé en base $2$, signifie :

$10_2 = 1 \times 2^1 + 0 \times 2^0 = 2_{10}$

10kind.jpg

Et le nombre $100111$ ?

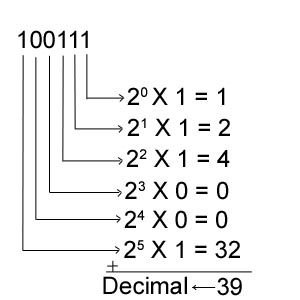
binaireToDec.gif

Remarque :

Tous les nombres dont l'écriture binaire se termine par $0$ sont pairs. Ceux se termiannt par $1$ sont impairs.

Exercice 3 :

Ecrire en base $10$ des nombres suivants :

  • $100_2$ :
  • $1101_2$ :
  • $11111111_2$:

Exercice 4 :

L'égalité suivante est-elle vraie :

$11001_2 \times 11_2 = 1001011_2$
  • Réponse :

Exercice 5 :

Quels nombres peut-on écrire en utilisant les puissances de $2$ jusqu'à $2^3$ (en allant donc de $0000_2$ à $1111_2$) ?

  • Réponse :

II.2 Binaire, bits et octets

En informatique, un bit, abbréviation de binary digit, est un $0$ ou un $1$. Un octet est un paquet de huit bits.

Attention aux abbréviations : en anglais, bit se dit bit (!) et s'abbrège avec b . Mais octet se dit byte et s'abbrège en B.

Par exemple, les débits internet de $9054$ Kbps (kilobits par seconde) et $1131,75$ Ko/sec (kilo-octets par secondes) sont égaux.

Si l'on code un nombre sur un octet (c.a.d. huit bits) on peut l'écrire avec au maximum huit chiffres ($0$ ou $1$). Le plus grand nombre possible sera alors $11111111_2=255_{10}$.

Exercice 6 :

Quel est le plus grand nombre que l'on puisse coder sur $4$ octets ?

  • Réponse :

III. Conversions :

On a déjà vu comment convertir un nombre en base $10$ vers la base $2$.

Et dans l'autre sens ?

  • Une première méthode consiste à décomposer le nombre en "paquets" correspondants à des puissances de $2$

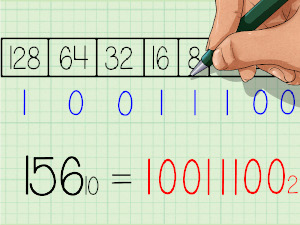
conversion1.jpg

Par exemple pour $154$ :

  • on peut mettre $128 = 2^7$. Il reste alors $26$
  • on ne peut pas mettre $64 = 2^6$ dans $26$
  • on ne peut pas mettre $32 = 2^5$ dans $26$
  • on peut mettre $16 = 2^4$ dans $26$. Il reste alors $10$
  • on peut mettre $8 = 2^3$ dans $10$. Il reste alors $2$
  • on ne peut pas mettre $4 = 2^2$ dans $2$
  • on peut mettre $2 = 2^1$ dans $2$. Il reste alors $0$
  • on ne peut pas mettre $1 = 2^0$ dans $0$

On a donc :

$154_{10} = 10011010_2$

Exercice 7 :

Utiliser cette technique afin d'écrire les nombres suivants en binaire :

  • $100_{10}$ :
  • $325_{10}$ :

Remarque : On peut vérifier ses calculs avec la fonction bin de python :

In [ ]:
# bin convertit un nombre entier donné en base 10 en son écriture binaire
# Le préfixe '0b' indique que le nombre est à lire en binaire
bin(100)
  • Une seconde méthode à utiliser des divisions euclidiennes (avec restes) par $2$ successives. A chaque étape, on note le reste de la division et l'on recommence avec le quotient. L'écriture binaire se retrouve en écrivant les restes à la suite en partant du dernier

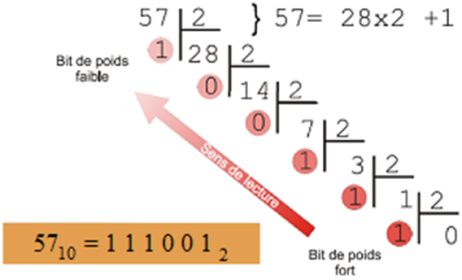
conversion2.png

Par exemple pour $154$ (le // indique que l'on fait une division euclidienne) :

  • $154\://\:2 = 77$. Le reste vaut $0$
  • $77\://\:2 = 38$. Le reste vaut $1$
  • $38\://\:2 = 19$. Le reste vaut $0$
  • $19\://\:2 = 9$. Le reste vaut $1$
  • $9\://\:2 = 4$. Le reste vaut $1$
  • $4\://\:2 = 2$. Le reste vaut $0$
  • $2\://\:2 = 1$. Le reste vaut $0$
  • $1\://\:2 = 0$. Le reste vaut $1$

On a donc :

$154_{10} = 10011010_2$

Remarque : On peut utiliser cette technique pour coder un programme convertissant les nombres de décimal vers binaire

Exercice 8 :

Utiliser cette technique afin d'écrire les nombres suivants en binaire :

  • $100_{10}$ :
  • $325_{10}$ :

IV. Opérations :

IV.1 Additions :

Les additions sont faciles à faire : on les pose comme en base $10$ mais on fait des retenues dès qu'une somme donne $2$ (une "deuzaine"). On retient alors $1$ dans la colonne suivante.

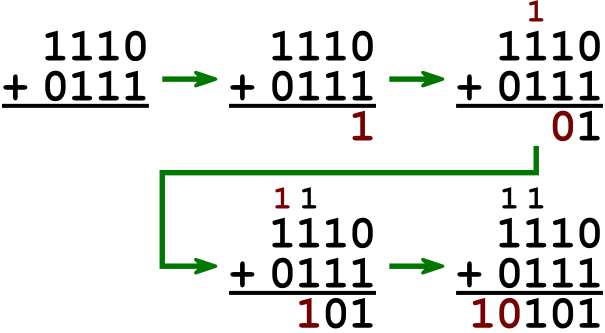
add-process.png

Exercice 9 :

Effectuer les additions suivantes :

1 0 1 1 0
+ 1 0 0 1 1
... ... ... ... ... ...

1 1 0 1 1
+ 1 1 0 0 1
... ... ... ... ... ...
In [6]:
# vérification avec python
# La fonction int convertit un nombre en binaire (donné sous forme de string) en un décimal
# On a précisé la base en second argument de int (cette fonction fonctionne avec d'autres bases : 3, 4, 5, ...)
resultat = int('10110',2) + int('10011',2)
bin (resultat)
Out[6]:
'0b101001'

IV.2 Soustractions :

Les soustractions sont un peu plus subtiles à cause des retenues.

  • On a bien sûr $1-0 = 1$, $0-0=0$ et $1-1=0$

  • Pour $0-1$ on doit faire une retenue :

    • On va chercher sur la gauche de la première ligne le premier $1$ et on le bascule à $0$. Le $0$ précédent est passé à $10$ ($2$ en décimal)
    • Si il faut encore décaler, ce $10$ est basculé à $1$ (on fait $2-1=1$) et le $0$ suivant à $10$
    • On recommence jusqu'à atteindre le calcul qui nous gênait initialement
    • Le $0-1$ qui posait problème devient $10-1 = 1$ ! En effet en binaire $10_2=2$ et $2-1=1$

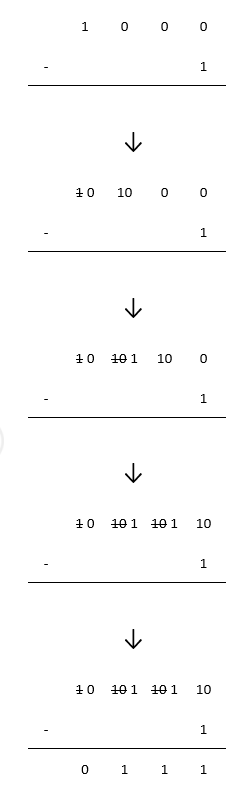
    soustraction.png

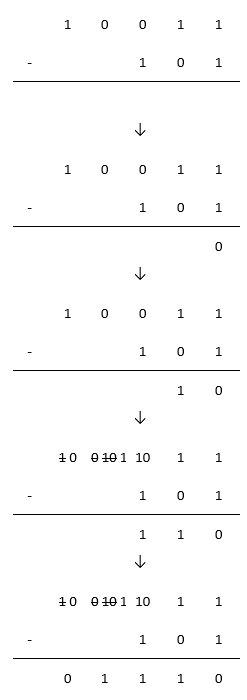
Ci-dessous la soustraction $10011-101$.

soustraction2.png

Exercice 9 :

Effectuer les soustractions suivantes :

  • $10101\:-\:100$ :
  • $101101\:-\:1011$ :
  • $1100001\:-\:11$ :
In [14]:
# vérification avec python
# La fonction int convertit un nombre en binaire (donné sous forme de string) en un décimal
# On a précisé la base en second argument de int (cette fonction fonctionne avec d'autres bases : 3, 4, 5, ...)
resultat = int('10010',2) - int('1101',2)
bin (resultat)
Out[14]:
'0b101'

V. La base 16 : l'héxadécimal

L'ordinateur utilise le codage binaire. Cette écriture est toutefois difficile à lire pour l'être humain.

Bien souvent, les nombres affichés à l'écran sont écrits en base $16$ : en héxadécimal. C'ets le cas par exemple pour les adresses MAC des appareils, pour la clé Wep d'une borne Wifi...

On doit donc écrire le nombre sous forme d'une série de coefficients entre $0$ et $16-1=15$.

Pour éviter les confusion entre le coefficient $10$ et la juxtaposition des coefficients $1$ et $0$, après $9$ on utilise des lettres :

$$1 \, \, \, 2 \, \, \, 3 \, \, \, 4 \, \, \, 5 \, \, \, 6 \, \, \, 7 \, \, \, 8 \, \, \, 9 \, \, \, a (10) \, \, \, b (11) \, \, \, c (12) \, \, \, d (13) \, \, \, e (14) \, \, \, f (15) $$

Ainsi le "nombre" $ab_{16}$ est égale à $10 \times 16 + 11 \times 1 = 171$

Un des grands avantages de la notation hexadécimale est sa facilité de conversion vers le binaire : chaque coefficient peut se lire comme un nombre binaire à quatre chiffres.

Par exemple, comme l'on a $a_16 = 10_{10} = 1010_{2}$ et $b_16 = 9_{10} = 1001_{2}$, on peut rapidement écrire : $$ ab_{16} = 1010 \: 1001_2 $$

In [ ]: