Généralités sur les algorithmes

I. Généralités :

I.1. Présentation :

Voici la définition que donne le Larousse d’un algorithme :

Ensemble de règles opératoires dont l'application permet de résoudre un problème énoncé au moyen d'un nombre fini d'opérations. Un algorithme peut être traduit, grâce à un langage de programmation, en un programme exécutable par un ordinateur

On distingue dès maintenant deux notions : l’algorithme et le programme:

  • l’algorithme est un ensemble de règles de calculs. Il peut s’exprimer dans plusieurs langages, en français, en anglais, en java ou python par exemple.
  • le programme quant à lui est la traduction de cet algorithme dans un certain langage. Les différentes qualités du langage (et du rédacteur du programme !) feront que le programme sera plus ou moins efficace (en terme de temps, de nombre d’opérations…).

languages.jpeg

Les objets de bases d’un algorithme sont les variables. Elles peuvent être de différents types. Retenons les suivantes :

  • Nombre entier (int)
  • Nombre décimal (ou à virgule flottante, float)
  • Chaîne de caractère (string)
  • Booléen (vrai/faux, bool)

Datatypes-in-Python.png

Les principales opérations réalisables par un algorithme sont les suivantes :

  • Affectation d’une valeur à une variable,
  • Lecture d’une valeur_ : l’utilisateur fournit une valeur à l’opérateur qui la stocke dans une variable,
  • Affichage à l’écran d’un message ou de la valeur d’une variable,
  • Test conditionnel : l’opérateur effectue un test (si …) et agit différemment selon que le résultat est vrai ou faux,
  • Itération : l’opérateur effectue une série d’action tant qu’une condition n’est pas réalisée,
  • Boucle « Pour » : l’opérateur effectue une série d’action pour toutes les valeurs d’une variable évoluant dans un certain ensemble.

I.2. Exemple :

Considérons le problème suivant : on souhaite écrire un programme calculant la moyenne de plusieurs nombres.

L'algorithme, écrit en pseudo-code est simple :

  • a, b, c et d sont des nombres

  • moyenne prend la valeur (a + b + c + d)/4

En python :

In [2]:
def moyenne_4_nb(a, b, c, d):
    """
    Calcule la moyenne des nombres a, b, c et d
    a, b, c et d sont des nombres
    Renvoie cette moyenne
    """
    
    moyenne = (a + b + c + d)/4
    
    return moyenne

Notez bien qu'à chaque définition de fonction, on ajoute un commentaire :

  • le rôle de la fonction
  • le type des variables
  • ce qu'elle renvoie

C'est la docstring. On y renviendra lorsque nous parlerons de spécifications d'une fonction

In [3]:
moyenne_4_nb(1, 2, 3, 4)
Out[3]:
2.5

Cela fonctionne.

Cette façon de faire a tout de même un gros désavantage : on ne calcule la moyenne que dans le cas de quatre nombres...

Pour gérer tous les cas de figures, on va utiliser une liste :

  • nombres est une liste de nombres

  • somme prend la valeur 0

  • Pour i allant de 0 à longueur(nombres) - 1

    • somme prend la valeur somme + nombres[i]

  • moyenne prend la valeur somme/longueur(nombres)

En python :

In [4]:
def moyenne_liste(nombres):
    """
    Calcule la moyenne des nombres de la liste nombres
    nombres est une liste de nombres
    Renvoie la moyenne
    """
    
    somme = 0
    
    for i in range(len(nombres)) :
        somme = somme + nombres[i]
    
    moyenne = somme / len(nombres) 
    
    return moyenne
In [5]:
moyenne_liste([1, 2, 3, 4])
Out[5]:
2.5
In [6]:
moyenne_liste([1, 2, 3, 4, 5, 6, 7])
Out[6]:
4.0

Pour information, voici le même programme codé dans différents langages :

  • En javascript (dans les pages web) :
function moyenne_liste(nombres) {
    var somme = 0;

    for (var i = 0; i < nombres.length; i++) {
        somme = somme + nombres[i];
    };

    moyenne = somme / nombres.length

    return moyenne;
}
  • En java (sur un téléphone Android) :
public float moyenne_liste(float[] nombres) {
    float somme = 0;

    for (int i = 0; i < nombres.length; i++) {
        somme = sommes + nombres[i];
    }

    moyenne = somme / nombres.length;

    return moyenne;
}
  • en PHP (sur un serveur web) :
function moyenne_liste($nombres) {

    $somme = 0;

    $longueur = count($nombres);

    for ($i = 0; $i < $longueur; $i++) {
         $somme = $somme + $nombres[i];
    }

    $moyenne = $somme / $longueur;

    return $moyenne;
   }

II. Correction d'un algorithme :

II.1. Spécifications :

Lorsque l'on définit une fonction, il est important de la documenter. Comme indiqué plus haut, on doit impérativement indiquer :

  • l'usage de la fonction
  • à quoi servent les paramètres et leurs types
  • ce que renvoie la fonction et de quel type

Le lien suivant propose les spécifications de la fonction sqrt (racine carrée) en C++ : https://www.programiz.com/cpp-programming/library-function/cmath/sqrt

Il existe plusieurs façon de présenter des documentations. Consulter à ce propos : https://stackoverflow.com/questions/3898572/what-is-the-standard-python-docstring-format

Ces informations permettent de décrire les spécifications de la fonction. Celles-ci comprennent :

  • le type des arguments et leur valeurs autorisées : ce sont les préconditions
  • le type de sortie et ce qu'elle est censée valoir : c'est la postcondition

Dans le cas de notre calcul de moyenne on a :

  • préconditions :
    • nombres est une liste de longueur non nulle
    • nombres ne contient que des nombres
  • postcondition :
    • la fonction renvoie la moyenne de tous les nombres de la liste fournie en argument

Nous devons donc adapter notre programme afin de tester les préconditions et aussi vérifier que la postcondition est toujours satisfaite.

Les préconditions peuvent être gérées à l'aide de assert :

assert CONDITION, "Message si la condition n'est pas remplie"

In [7]:
def moyenne_liste_V2(nombres):
    """
    Calcule la moyenne des nombres de la liste nombres
    nombres est une liste de nombres
    Renvoie la moyenne
    """
    
    # On teste si nombres est une liste avec isinstance (variable "is instance of" type)
    assert isinstance(nombres, list), "L'argument doit être une liste"
    
    # On teste si la liste est non-vide
    assert len(nombres) > 0, "La liste doit être non vide"
    
    # On vérifie que tous les éléments sont des nombres entiers ou flottants
    for n in nombres :
        assert isinstance(n, (int, float)), "Les éléments de la liste doivent tous être des nombres"
    
    somme = 0
    
    for i in range(len(nombres)) :
        somme = somme + nombres[i]
    
    moyenne = somme / len(nombres) 
    
    return moyenne

Pour tester notre codage, on peut dès lors utiliser un jeu de test. Il s'agit d'un ensemble de valeurs à donner à notre fonction permettant de vérifier son bon fonctionnement et sa bonne gestion des exceptions.

In [8]:
# Test avec une valeur
moyenne_liste_V2([10])
Out[8]:
10.0
In [9]:
# Test avec deux valeurs
moyenne_liste_V2([1,2])
Out[9]:
1.5
In [10]:
# Test avec 1000 valeurs !
moyenne_liste_V2(list(range(1000)))
Out[10]:
499.5
In [11]:
# On donne des flottants
# Notez au passage l'erreur de calcul propre au traitement des flottants par Python
moyenne_liste_V2([0.1, 0.2])
Out[11]:
0.15000000000000002
In [12]:
# On donne des entiers et des flottants
moyenne_liste_V2([5, 7.8])
Out[12]:
6.4
In [13]:
# On donne autre chose qu'une liste
moyenne_liste_V2(5)

---------------------------------------------------------------------------
AssertionError                            Traceback (most recent call last)
<ipython-input-13-cca45eacceb4> in <module>
      1 # On donne autre chose qu'une liste
----> 2 moyenne_liste_V2(5)

<ipython-input-7-5a0547dce536> in moyenne_liste_V2(nombres)
      7 
      8     # On teste si nombres est une liste avec isinstance (variable "is instance of" type)
----> 9     assert isinstance(nombres, list), "L'argument doit être une liste"
     10 
     11     # On teste si la liste est non-vide

AssertionError: L'argument doit être une liste
In [14]:
# On donne une liste vide
moyenne_liste_V2([])

---------------------------------------------------------------------------
AssertionError                            Traceback (most recent call last)
<ipython-input-14-0a7158918481> in <module>
      1 # On donne une liste vide
----> 2 moyenne_liste_V2([])

<ipython-input-7-5a0547dce536> in moyenne_liste_V2(nombres)
     10 
     11     # On teste si la liste est non-vide
---> 12     assert len(nombres) > 0, "La liste doit être non vide"
     13 
     14     # On vérifie que tous les éléments sont des nombres entiers ou flottants

AssertionError: La liste doit être non vide
In [16]:
# On donne un élément non numérique
moyenne_liste_V2([5, 3, 'a'])

---------------------------------------------------------------------------
AssertionError                            Traceback (most recent call last)
<ipython-input-16-58e928450d4f> in <module>
      1 # On donne un élément non numérique
----> 2 moyenne_liste_V2([5, 3, 'a'])

<ipython-input-7-5a0547dce536> in moyenne_liste_V2(nombres)
     14     # On vérifie que tous les éléments sont des nombres entiers ou flottants
     15     for n in nombres :
---> 16         assert isinstance(n, (int, float)), "Les éléments de la liste doivent tous être des nombres"
     17 
     18     somme = 0

AssertionError: Les éléments de la liste doivent tous être des nombres

Notre fonction passe bien l'ensemble des tests.

Bien entendu, il est impossible de tester tous les cas de figures (ici il faudrait tester toutes les moyennes possibles !). Il ne faut donc pas oublier qu'un jeu de tests est toujours incomplet.

Le module python unittest (https://docs.python.org/3.5/library/unittest.html#module-unittest) permet de formaliser les jeux de tests.

Pour la postcondition, la vérification ici est facile : la boucle for parcourt et additionne l'ensemble des valeurs de la liste nombres et la moyenne est égale à cette somme divisée par le nombre d'éléments de nombres. On calcule bien la moyenne.

II.2. Terminaison et correction partielle :

Lorsque l'on rédige un programme on doit s'assurer que celui-ci :

  • se termine
  • produit la valeur attendue

Ces deux conditions sont appelées :

  • terminaison
  • correction partielle

Démontrer la correction d'un algorithme, c'est démontrer sa terminaison et sa correction partielle

II.2.1 Terminaison :

La terminaison est subtile : nous devons nous assurer que l'algorithme s'arrêtera à un moment.

Si l'algorithme ne comporte pas de boucle, c'est immédiat : une fois que toutes les instructions ont été traitées, le programme s'arrête.

Cela se complique si l'on a des boucles Pour et surtout Tant Que. On doit alors faire intervenir une nouvelle notion : le variant de boucle.

Il s'agit :

  • d'un nombre entier strictement positif manipulé par la boucle
  • qui décroît strictement à chaque tour de boucle

Etant obligatoirement strictement décroissant et strictement positif, on est certain que notre variant de boucle atteindra $0$ : on sort alors de la boucle et l'algorithme peut se terminer.

Dans le cas d'une boucle Pour, le variant de boucle classique est le nombre d'itérations restant à faire.

Par exemple si $i$ prend toutes les valeurs entre $0$ et $10$, on peut prendre comme variant de boucle $10-i$. C'est bien un nombre entier strictement positif et décroissant :

  • lors de la 1ère itération, $i$ vaut $0$ et $10-i$ vaut $10$
  • lors de la 2ème itération, $i$ vaut $1$ et $10-i$ vaut $9$
  • ...
  • lors de la 11ème itération, $i$ vaut $10$ et $10-i$ vaut $0$ : la boucle s'arrête

Dans le cas d'une boucle Tant que, c'est moins évident. Imaginons le code suivant :

  • n est un nombre saisit par l'utilisateur
  • s est une chaîne de caractère vide
  • Tant que n est strictement positif :
    • si n est pair :
      • s prend la valeur 0 + s
      • n prend la valeur n/2
    • sinon :
      • s prend la valeur 1 + s
      • n prend la valeur (n-1)/2

Il s'agit de l'algorithme convertissant un nombre entier en binaire.

Quel variant de boucle choisir ? On peut prendre $n$ mais il faut s'assurer que c'est bien en entier strictement positif et décroissant :

  • $n$ est initialement un entier (cela fait partie des préconditions)
  • à chaque itération, on teste la parité de $n$
    • s'il est pair, on le divise par $2$. On reste dans les entiers et $n$ a décru
    • sinon, s'il est imppair, on lui soustrait $1$ puis on le divise par $2$. On reste dans les entiers et $n$ a décru
  • on sort de la boucle quand $n$ vaut $0$ : cette valeur sera obligatoirement atteinte

II.2.2 Correction partielle :

La correction partielle revient à vérifier que la postcondition est satisfaite.

Pour ce faire nous devons définir un invariant de boucle. Il s'agit d'une propriété/affirmation qui :

  1. est vérifié avant l'entrée d'une boucle
  2. s'il est vérifié avant une itération est vérifié après celle-ci
  3. lorsqu'il est vérifié à la sortie d'une boucle permet d'en déduire que le programme est correct

Dans le cas de notre calcul de moyenne, la boucle while porte sur la somme. Nous prendrons la propriété suivante :

$$P_k \: : \: "A \: l'issue \: de \: l'itération \: k \: de \: la \: boucle, \: la \: somme \: est \: égale \: à \: la \: somme \: des \: k \: premières \: valeurs"$$

Pour prouver que cette invariant est toujours vraie, on utilise le raisonnement par récurrence. Ce type de raisonnement mathématique consiste à :

  1. Vérifier que la propriété est initialement vraie (initialisation)
  2. Supposer que la propriété est vraie à un certain rang (hypothèse de récurrence)
  3. Montrer qu'elle est obligatoirement vraie au rang suivant (hérédité)

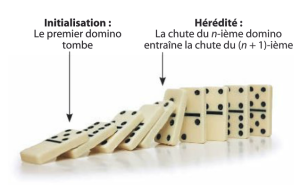
On peut envisager ce genre de démonstration à l'aide d'une chute de domino :

  • on fait tomber le premier domino (initialisation)
  • on a placé tous les dominos de façon à ce que si un domino tombe (hypothèse de récurrence) alors le suivant tombe aussi (hérédité)

TS_suites_dominos.png

Voici la démonstration pour notre calcul de moyenne :

  1. Avant d'entrer dans la boucle, la somme vaut $0$ : c'est bien la somme des $0$ premières valeurs. La propriété est initialisée
  2. On suppose qu'à l'issue de la $k$-ième boucle, somme contient la somme des $k$ premières valeurs, de $0$ à $k-1$ (hypothèse de récurrence)
  3. On fait fonctionner la $(k+1)$-ième itération de la boucle. Celle-ci additionne la valeur de rang $k$ à somme qui est alors égale à la somme des $k+1$ premières valeurs, de $0$ à $k$. On a bien prouver l'hérédité.

Notre invariant de boucle est donc bien initialisé et héréditaire : il est vrai à chaque tour de boucle. On a donc prouver la correction partielle de notre algorithme.

III. Complexité d'un algorithme :

III.1. Présentation générale :

Lorsque l'on écrire un algorithme effectuant une tâche donnée plusieurs méthodes s'offrent à nous.

Considérons le problème suivant : on cherche si un nombre est présent dans une liste triée de nombres.

Une première méthode est de parcourir tous les éléments du premier au dernier et de s'arrêter dès que l'on a soit :

  • trouver le nobre cherché
  • dépassé la valeur cherchée

En python (on n'écrit pas les tests de préconditions) :

In [18]:
def cherche_valeur(liste, valeur) :
    """
    Cherche la valeur indiquée dans la liste proposée
    liste est une série de valeurs numériques triées
    valeur est une valeur numérique à chercher
    Renvoie True si la valeur est présente, False sinon
    """
    
    for n in liste :
        if n == valeur :
            return True
        elif n > valeur :
            return False
    
    return False
In [19]:
cherche_valeur([1,2,5] , 5)
Out[19]:
True
In [20]:
cherche_valeur([1,2,5] , 8)
Out[20]:
False
In [21]:
cherche_valeur([1,2,5] , 1.5)
Out[21]:
False

Une autre façon de faire nécessite :

  • regarder l'élément du milieu
    • s'il est strictement plus grand que la valeur cherchée, on reprend la recherche sur les valeurs du début
    • s'il est plus petit que la valeur cherchée, on reprend la recherche sur les valeurs de la fin
  • recommencer la recherche avec la nouvelle liste jusqu'à ce que l'on soit face à un intervalle de recherche d'une valeur
  • renvoyer le résultat de la comparaison entre la valeur à trouver et le dernier élément de la zone de recherche

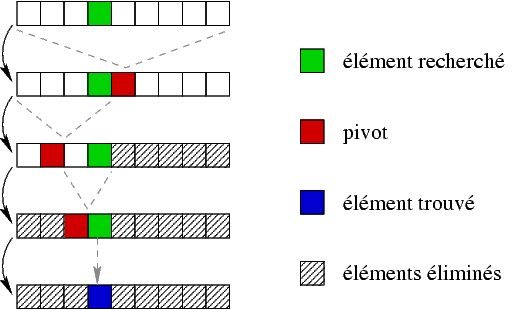
fig-dichotomie.gif

C'est la recherche dichotomique. En python :

In [22]:
def cherche_valeur_dicho(liste, valeur) :
    debut = 0
    fin = len(liste) - 1
    
    while debut != fin :
        # indice du milieu
        milieu = (fin + debut)//2
        
        if liste[milieu] > valeur :
            fin = milieu # on cherche sur le début de la liste
        else :
            debut = milieu + 1
    
    return liste[debut] == valeur
In [23]:
cherche_valeur_dicho([1,2,5] , 5)
Out[23]:
True
In [24]:
cherche_valeur([1,2,5] , 8)
Out[24]:
False
In [25]:
cherche_valeur([1,2,5] , 1.5)
Out[25]:
False

Ce sont deux méthodes très différentes. On peut se demander laquelle est la plus efficace.

Le concept informatique décrivant cette question est la complexité.

Il existe deux types de complexité :

  • la complexité en mémoire. Quelle place dans la mémoire, cette méthode nécessite-t-elle ?
  • la complexité en calcul. Combien d'opérations cette méthode nécessite-t-elle ?

Nous n'étudierons que la complexité en calcul.

Une première approche revient à regarder le temps de calcul nécessaire à chaque fonction.

In [26]:
# Génération d'une liste triée de 100 nombres et d'un élément à chercher au hasard dans cette liste
# Relancer cette cellule pour refaire des tests
from random import randint

liste = list(range(100))
valeur = randint(0,100)

%timeit cherche_valeur(liste, valeur)

%timeit cherche_valeur_dicho(liste, valeur)

3.53 µs ± 64.1 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)
1.95 µs ± 26.9 ns per loop (mean ± std. dev. of 7 runs, 1000000 loops each)

Les durées sont très différentes et il semble que la première méthode soit beaucoup plus rapide.

Refaisons des essais dans le pire des cas. Ici ce serait si la valeur à chercher est la dernière de la liste :

In [27]:
# Génération d'une liste triée de 100 nombres et d'un élément à chercher au hasard dans cette liste
# Relancer cette cellule pour refaire des tests
from random import randint

liste = list(range(100))
valeur = 99

%timeit cherche_valeur(liste, valeur)

%timeit cherche_valeur_dicho(liste, valeur)

10.1 µs ± 462 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)
2.17 µs ± 110 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)

Le temps de calcul a augmenté pour la première méthode (on pouvvait s'y attendre) mais pas pour la seconde : elle n'a pas fait plus d'opérations.

III.2. Calcul de la complexité :

Déterminer la complexité en calcul d'un algorithme est une chose ardue. Nous le ferons dans des cas simples.

Il faut tout d'abord compter le nombres d'opérations nécessaires à l'algorithme pour se terminer. On fait ce calcul dans le pire des cas.

On appelle $n$ le nombre de valeurs du tableau dans lequel on cherche.

Dans le cas de la recherche "simple" il faut :

  • Pour chacun des éléments de la liste (il y en a $n$) :
    • tester son égalité avec la valeur cherchée ($1$ opération)
    • tester s'il est supérieur à la valeur cherchée ($1$ opération)

On a donc en tout $n \times (1 + 1) = 2n$ opérations.

Remarque : on néglige certaines opérations comme le return et les opérations propres à la boucles for

On voit que le nombre d'opération s'exprimer sous forme d'une fonction (un polynôme) dont la puissance la plus grande est $1$ (le $n$ est à la puissance $1$).

On dira que notre algorithme est de complexité linéaire que l'on note $\mathcal{O}(n)$.

Notre deuxième méthode est plus compliquée. Son nombre d'opérations est lié au nombre de division par deux de la zone de recherche qu'elle peut faire.

La fonction mathématique $\log_2$ (logarithme de $2$, vu en Terminale) donne ce nombre.

On dira que notre algorithme est de complexité logarithmique que l'on note $\mathcal{O}(\log_2(n))$.

III.3. Les différentes classes de complexité :

Il existe de nombreux algorithmes différents et donc de nombreux cas de complexité différents.

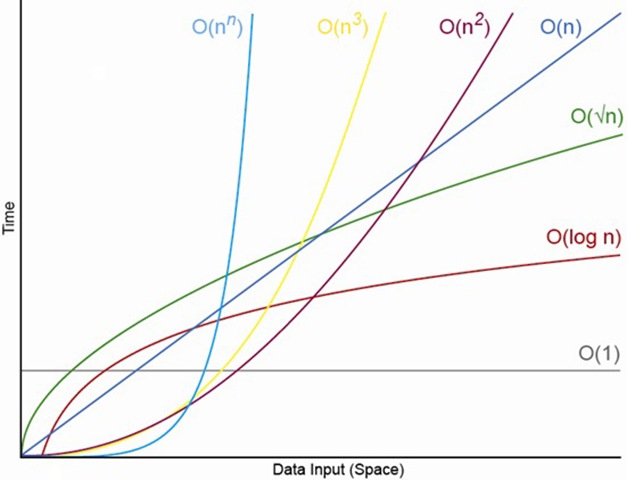
Le tableau suivant, adapté de Wikipedia (https://fr.wikipedia.org/wiki/Analyse_de_la_complexit%C3%A9_des_algorithmes#Complexit%C3%A9,_comparatif), présente plusieurs cas :

complexit%C3%A9Court.PNG

La complexité a un impact immédiat sur le temps de calcul :

  • pour une complexité linéaire, si on multiple la taille des valeurs par $5$, le nombre d'opérations (et le temps de calcul) est mulpitiplié par $5$
  • pour une complexité quadratique $\mathcal{O}(n^2)$, si multiple la taille des valeurs par $5$, le nombre d'opérations (et le temps de calcul) est multiplié par $25 = 5^2$
  • pour une complexité factorielle $\mathcal{O}(n!)$, si on multiple la taille des valeurs par $5$, le nombre d'opérations (et le temps de calcul) est multiplié par $ 120 = 5 \times 4 \times 3 \times 2 \times 1$

complexit%C3%A9.jpg

Notre première méthode de recherche est en complexité linéaire : comparons les temps de calculs si on multiplie la taille des données par $10$ :

In [28]:
# Génération d'une liste triée de 100 nombres et d'un élément à chercher au hasard dans cette liste
# Relancer cette cellule pour refaire des tests
liste = list(range(100))
valeur = 99

%timeit cherche_valeur(liste, valeur)

10.3 µs ± 342 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)
In [29]:
# Génération d'une liste triée de 1000 nombres et d'un élément à chercher au hasard dans cette liste
# Relancer cette cellule pour refaire des tests
liste = list(range(1000))
valeur = 999

%timeit cherche_valeur(liste, valeur)

97.4 µs ± 2.3 µs per loop (mean ± std. dev. of 7 runs, 10000 loops each)

Remarque : le graphique précédent laisse penser que la complexité logarithmique (celle de la recherche dichotomique) devient meilleure que la complexité linéaire quand la taille des données augmente. Testons :

In [30]:
# Génération d'une liste triée de 100 000 nombres et d'un élément à chercher au hasard dans cette liste
# Relancer cette cellule pour refaire des tests
liste = list(range(100_000))
valeur = 99_999

%timeit cherche_valeur(liste, valeur)

%timeit cherche_valeur_dicho(liste, valeur)

9.58 ms ± 118 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
5.65 µs ± 33.9 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)