Tri par insertion et par sélection

On considère dans ce cours le tri d'un tableau de valeurs. Celles-ci peuvent être de types différents :

  • nombres
  • chaînes de caractères
  • ...

On considérera ici le cas de nombres entiers.

In [4]:
from random import shuffle

def melange_tableau(taille) :
    """
    Création d'un tableau mélangé d'entiers entre 0 et taille - 1
    Prend en entrée la taille du tableau (entier >= 1)
    Renvoie le tableau mélangé
    """
    
    # Génération du tableau non mélangé
    tableau = list(range(taille))

    # Mélange du tableau
    shuffle(tableau)
    
    return tableau
In [5]:
tableau = melange_tableau(100)

print(tableau)

[31, 39, 29, 51, 16, 41, 58, 83, 0, 43, 59, 66, 7, 82, 23, 75, 44, 93, 97, 85, 71, 79, 61, 46, 9, 28, 19, 17, 4, 32, 73, 15, 56, 48, 26, 2, 84, 88, 45, 52, 87, 1, 95, 90, 37, 69, 62, 92, 10, 86, 47, 8, 12, 64, 6, 49, 81, 96, 55, 50, 77, 18, 89, 35, 24, 53, 91, 65, 40, 54, 21, 5, 36, 57, 30, 27, 68, 38, 63, 98, 74, 60, 22, 94, 80, 25, 78, 3, 34, 72, 67, 76, 42, 99, 20, 33, 11, 14, 70, 13]

On obtient ainsi un tableau contenant les entiers entre $0$ et $99$ qu'il va s'agir de trier dans l'ordre croissant.

On pourra compléter la lecture de ce cours par la visite de différents sites internet :

I. Tri par sélection :

I.1. Présentation :

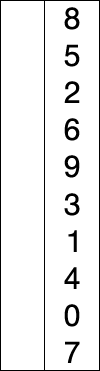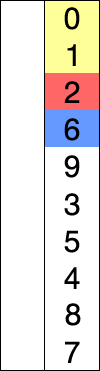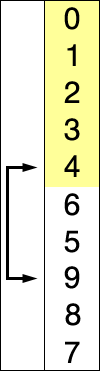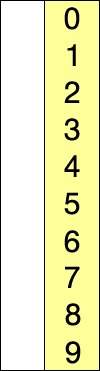
C'est le tri du joueur de carte : à chaque étape on parcourt l'ensemble des cartes restant à trier pour trouver la plus petite et onla place au début de la liste.

Le pseudo-code est le suivant :

  • tableau est le tableau des valeurs à trier

  • Pour i allant de 0 jusqu'à longueur du tableau - 2 :

    • indice_min prend la valeur i

    • Pour j allant de i+1 jusqu'à longueur du tableau - 1 :

      • Si tableau[j] < tableau[indice_min] :

        • indice_min prend la valeur j

    • Echanger les valeurs tableau[i] et tableau[indice_min]

Selection-Sort-Animation.gif

selection.gif

En python :

In [7]:
def tri_selection(tab) :
    """
    Tri le tableau d'entiers tab par sélection
    Renvoie le tableau trié
    """
    
    for i in range(len(tab)-1) :
        indice_min = i
        for j in range(i+1, len(tab)) :
            if tab[j] < tab[indice_min] :
                indice_min = j
        tab[i], tab[indice_min] = tab[indice_min], tab[i]
    
    return tab
In [9]:
tableau = melange_tableau(100)
print(tableau)

[69, 30, 67, 81, 93, 74, 49, 35, 54, 64, 45, 2, 32, 1, 19, 31, 56, 73, 11, 53, 3, 4, 83, 78, 18, 99, 84, 90, 24, 12, 85, 91, 38, 97, 95, 28, 68, 25, 37, 44, 29, 94, 63, 20, 79, 36, 66, 75, 88, 89, 13, 0, 70, 8, 62, 43, 59, 58, 42, 7, 76, 96, 77, 50, 60, 47, 80, 92, 14, 6, 23, 41, 5, 51, 98, 87, 46, 21, 17, 86, 48, 61, 9, 15, 16, 27, 65, 71, 39, 22, 52, 34, 72, 57, 33, 55, 40, 10, 26, 82]
In [12]:
print(tri_selection(tableau))

[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99]

I.2. Caractéristiques :

Il s'agit d'un tri en place : les éléments sont triés directement dans le tableau initial.

Ce n'est pas un tri stable : si deux éléments étaient égaux, celui apparaissant initialement en premier dans le tableau porrait ressortir en second à l'issue du tri.

Est-on sûr que cet algorithme s'arrête ? On peut choisir comme invariant de boucle la proposition suivante :

$$Au \: i-ème \: tour \: de \: boucle \:, les \: éléments \: de \: 0 \: à \: i-1 \: sont \: triés$$

Cette propriété est toujours vraie :

  • Initialisation :
    • au $1er$ tour le boucle, l'élément d'indice $0$ est trié (c'est le seul)
  • Hérédité :
    • on suppose que l'on a atteint la $i-ème$ boucle et donc que les éléments d'indices $0$ à $i-1$ sont triés
    • au $(i+1)-ème$ tour de boucle, on trouve le plus petit élément entre $i$ et la fin du tableau et on le place à l'indice $i$. Les éléments d'indices $0$ à $i$ sont donc bien triés

Qu'en est-il de la complexité ? On note $n$ la taille du tableau.

  • Au premier tour de boucle le programme doit lire et comparer tous les nombres d'indices entre $0$ et $n-1$. Cela fait $n$ comparaisons

  • Au deuxième tour de boucle le programme doit lire et comparer tous les nombres d'indices entre $1$ et $n-1$. Cela fait $n-1$ comparaisons

  • Au troisième tour de boucle le programme doit lire et comparer tous les nombres d'indices entre $2$ et $n-1$. Cela fait $n-2$ comparaisons

  • ...

  • Au dernier tour de boucle le programme doit lire et comparer tous les nombres d'indices entre $n-1$ et $n-1$. Cela fait $1$ comparaison

Il y a donc en tout : $$(n-1) + (n-2) + (n-3) + \dots + 2 + 1$$ comparaisons.

Une formule de mathématiques montre que cette somme vaut $\frac{n(n-1)}{2} = \frac{1}{2}n^2-\frac{1}{2}n$

On voit que le terme dominant est $n^2$ : cet algorithme est de complexité quadratique $\mathcal{O}(n^2)$

Cela implique que si l'on multiplie la taile des données par $10$, le nombre d'opération et donc temps d'éxécution seront multiplié par un facteur $10^2=100$ :

In [13]:
# Tableau de taille 100
tableau = melange_tableau(100)
In [14]:
%timeit tri_selection(tableau)

662 µs ± 27.7 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)
In [15]:
# Tableau de taille 1000
tableau = melange_tableau(1000)
In [16]:
%timeit tri_selection(tableau)

71.3 ms ± 2.21 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)
In [17]:
# Tableau de taille 10 000
tableau = melange_tableau(10_000)
In [18]:
%timeit tri_selection(tableau)

6.94 s ± 237 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)

II. Tri par insertion :

II.1. Présentation :

La démarche est assez classique : à chaque étape on sort une valeur et on la place à sa position dans la partie gauche de la liste. On passe ensuite à la valeur suivante.

Le pseudo-code est le suivant :

  • tableau est le tableau des valeurs à trier

  • Pour i allant de 0 jusqu'à longueur du tableau - 1 :

    • Pour j allant de i jusqu'à 1 (à rebours):

      • Si tableau[j-1] > tableau[j] :

        • Echanger les valeurs tableau[j-1] et tableau[j]

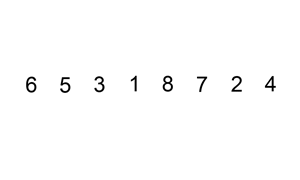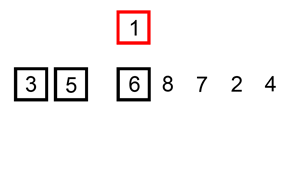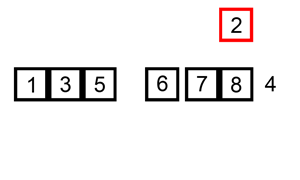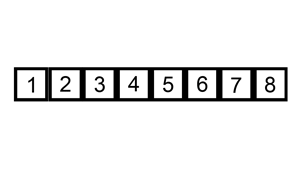
Insertion-sort-example-300px.gif

insertion.gif

En python :

In [19]:
def tri_insertion(tab) :
    """
    Tri le tableau d'entiers tab par insertion
    Renvoie le tableau trié
    """
    
    for i in range(len(tab)) :
        for j in range(i, 0, -1) :
            if tab[j-1] > tab[j] :
                tab[j-1], tab[j] = tab[j], tab[j-1]
    
    return tab
In [20]:
tableau = melange_tableau(100)
print(tableau)

[24, 54, 67, 48, 10, 81, 39, 50, 77, 2, 34, 44, 8, 49, 92, 35, 5, 55, 53, 1, 87, 78, 70, 60, 17, 4, 89, 91, 42, 9, 51, 19, 72, 59, 41, 12, 3, 30, 13, 20, 99, 97, 62, 80, 45, 82, 68, 69, 90, 0, 95, 84, 94, 85, 11, 93, 64, 23, 37, 31, 61, 66, 46, 57, 7, 16, 75, 58, 32, 86, 18, 71, 38, 36, 79, 65, 96, 43, 26, 52, 47, 33, 73, 63, 40, 83, 14, 15, 76, 56, 74, 6, 28, 98, 22, 21, 88, 25, 27, 29]
In [21]:
print(tri_insertion(tableau))

[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99]

II.2. Caractéristiques :

Il s'agit d'un tri en place : les éléments sont triés directement dans le tableau initial

C'est pas un tri stable : si deux éléments sont égaux, ils ne changent pas de place à l'issue du tri

Est-on sûr que cet algorithme s'arrête ? On peut choisir comme invariant de boucle la proposition suivante :

$$Au \: i-ème \: tour \: de \: boucle \:, les \: éléments \: de \: 0 \: à \: i-1 \: sont \: triés$$

Cette propriété est toujours vraie :

  • Initialisation :
    • au $1er$ tour le boucle, l'élément d'indice $0$ est trié (c'est le seul)
  • Hérédité :
    • on suppose que l'on a atteint la $i-ème$ boucle et donc que les éléments d'indices $0$ à $i-1$ sont triés
    • au $(i+1)-ème$ tour de boucle, on insère le $i-ème$ élément à sa position entre la position $0$ et $i$. Les éléments d'indices $0$ à $i$ sont donc bien triés

Qu'en est-il de la complexité ? On note $n$ la taille du tableau. On se place dans le pire des cas : le tableau est initialement trié dans l'ordre décroissant.

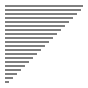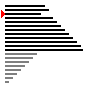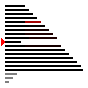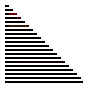
animation%20of%20insertion%20algorithms.gif

  • Au premier tour de boucle le programme doit échanger les valeurs d'indices $0$ et $1$. Cela fait $1$ échange (le $0$ à la place du $1$)

  • Au deuxième tour de boucle le programme doit échanger les valeurs d'indices $0$, $1$ et $2$. Cela fait $2$ échanges (le $2$ à la place du $1$ puis le $1$ à la place du $0$)

  • Au troisième tour de boucle le programme doit échanger les valeurs d'indices $0$, $1$, $2$ et $3$. Cela fait $3$ échanges (le $3$ à la place du $2$ ...)

  • ...

  • Au troisième tour de boucle le programme doit échanger les valeurs d'indices $0$, $1$, $2$, ... et $n-1$. Cela fait $n-1$ échanges

Il y a donc en tout : $$1 + 2 + 3 + \dots + (n-1)$$ comparaisons.

Là encore cela donne $\frac{n(n-1)}{2} = \frac{1}{2}n^2-\frac{1}{2}n$

Le terme dominant est toujours $n^2$ : cet algorithme est de complexité quadratique $\mathcal{O}(n^2)$

In [22]:
# Tableau de taille 100
tableau = melange_tableau(100)
In [23]:
%timeit tri_insertion(tableau)

796 µs ± 60.1 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)
In [24]:
# Tableau de taille 1000
tableau = melange_tableau(1000)
In [25]:
%timeit  tri_insertion(tableau)

88.9 ms ± 1.35 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)
In [26]:
# Tableau de taille 10 000
tableau = melange_tableau(10_000)
In [27]:
%timeit  tri_insertion(tableau)

9.9 s ± 257 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)

Il existe de nombreux autres algorithmes de tri, certains, beaucoup plus efficaces que les deux présentés ci-dessus :

animation%20of%20sorting%20algorithms.gif