Valeurs booléennes
On souhaite que l'ordinateur soit une machine exacte : si on lui propose une affirmation, on souhaite qu'il soit capable de juger de sa valeur de vérité.
Beaucoup de mathématiciens et de philosophes (Aristote, Leibniz...) ont réfléchi aux règles du raisonnement correct : c'est ce que l'on appelle la logique.
Parmi tous ces noms, celui de George Boole (1815 - 1864) sort du lot. Il a durant sa vie formalisé la logique moderne sous la forme de ce que nous appelons encore aujourd'hui la logique de Boole.

I. Des 0 et des 1 :¶
Les éléments de base de logique de Boole sont les valeurs booléenes. Il n'y en a que deux :
- $0$ ou
False(Faux) - $1$ ou
True(Vrai)
Python connaît ces valeurs :
True
False
bool(0)
bool(1)
Ces valeurs sont des affirmations. Elles sont les réponses à des questions que l'on pose à l'ordinateur :
# 3 est-il plus grand que 0 ?
3 > 0
# 3 est-il plus grand que 5 ?
3 > 5
# Si a vaut 8, est-ce que 2a vaut 17 ?
a = 8
2*a == 17
# Est-ce que le 0 est bien égal à False ? Python répond True car c'est vrai
0 == False
# Est-ce que le '0' est bien égal à False ? Python répond False car c'est faux
# ('0' en caractère et non entier)
'0' == False
II. Opérateurs logiques :¶
Il est régulièrement intéressant de poser des questions plus élaborées. Par exemple : est-ce que la valeur de $x$ est comprise entre $5$ et $12$ ?
En fait cette question est double. On demande que : "$x$ soit plus grand que $5$" ET "$x$ soit plus petit que $12$"
En python on tape :
# on donne une valeur à x pour tester la question
x = 10
(x > 5) and (x < 12)
# on donne une valeur à x pour tester la question
x = 20
(x > 5) and (x < 12)
On l'a compris, les seuls nombres permettant de répondre True à cette question, sont les valeurs de $]5\:;\:12[$. Pour que la proposition soit True, il faut que les deux sous-propositions soient True en même temps.
Cela nous ammène à construire la table de vérité de l'opération "ET", ou plutôt and :
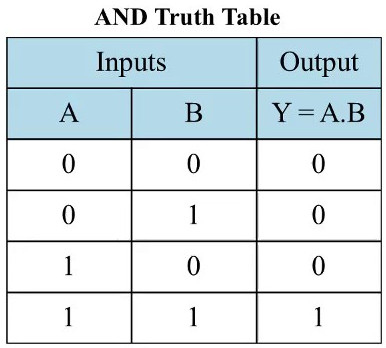
La lecture est facile. Dans la première ligne on considère le cas où $A$ et $B$ valent $0$ (Faux). $A\:et\:B$ vaut donc $0$ (Faux).
Cette loi est noté avec le point : $A\:.\:B$
Il existe d'autres opérateurs logiques :
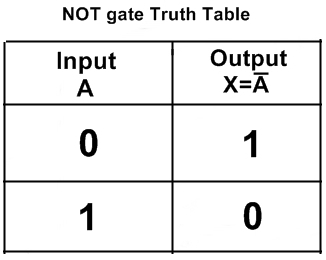
- Non /
not: $\overline{A}$
On nie simplement la valeur booléenne
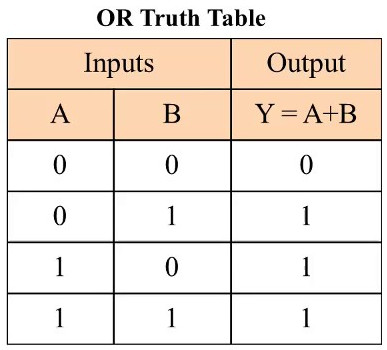
- Ou /
or: $A\:+\:B$
Au moins l'une des deux valeurs booléennes est vraie
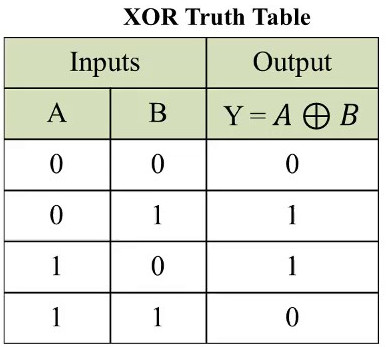
- Ou exclusif /
xor: $A\:\bigoplus\:B$
Excatement l'une des deux valeurs booléennes est vraie (comme le "Fromage ou Dessert" du restaurant, pas les deux !)
On peut alors créer des questions compliquées :
# On veut l'inverse de 3 > 5 qui est Faux. Donc on obtient Vrai
not (3 > 5)
# Est-ce que 3 est plus grand que 5 ou 'a' est avant 'b' dans l'ordre alphabetique ?
(3 > 5) or ('a' < 'b')
# Attention 'a' < 'b' est du pur python. Pas sûr que cela marche dans d'autres langages !
# Quelle est la négation de "5 est-il plus grand que 3 ?" ET "8 est-il plus petit que 12 ?"
not ((5 > 3) and (8 < 12))
# "3 > 1" OU EXCLUSIF "3 > 0". Comme les deux sont vraies on obtient faux
(3 > 1) ^ (3 > 0)
# "3 > 1" OU EXCLUSIF "3 < 0". Comme seulement une est vraie on obtient vrai
(3 > 1) ^ (3 < 0)
# Le symbole du XOR en python est donc le ^
Cela devient un peu laborieux lorsque l'on complique les questions. Heureusement il est possible de simplifier les choses avec des règles de calcul :
- Les parenthèses sont prioritaires
- On peut distribuer les opérateurs comme on distribue la multiplication
- La négation d'un ET est un OU et vice-versa
Par exemple, en prenant $P$, $Q$ et $R$ comme des affirmations (du type "3 > 2" ou "5 < 2") :
- non ($P$ et $Q$) = (non $P$) ou (non $Q$)
- $P$ et ($Q$ ou $R$) = ($P$ et $Q$) ou ($P$ et $R$)
Un dernier pour se prendre la tête :
- non ($P$ ou ($Q$ et (non $R$)) = non ( ($P$ ou $Q$) et ($P$ et (non $R$)) = ((non $P$) et (non $Q$)) ou ((non $P$) ou $R$)
Plus concrètement, que dire de l'affirmation : non (($3 > 5$) et ($8 > 2$)) ?
C'est la même affirmation que : non ($3 > 5$) ou non ($8 > 2$)
C'est à dire : ($3 \le 5$) ou ($8 \le 2$)
C'est donc vrai car $3$ est bien plus petit que $5$.
not ((3 > 5) and (8 > 2))
III. Tables de vérité d'expressions boolénnes :¶
Considérons l'affirmation suivante ($A$ et $B$ sont des affirmations): $$ (E)\:\:: (\:non\:A\:)\:ou\:(\:non\:B\:) $$
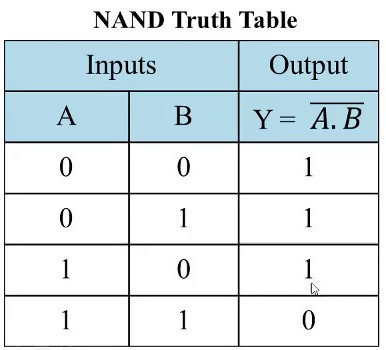
Ce sera notre nouvel opérateur. Appelons-le $net$. Quelle est sa table de vérité ?
| $A$ | $B$ | $net$ |
|---|---|---|
| $0$ | $0$ | $1$ |
| $0$ | $1$ | $1$ |
| $1$ | $0$ | $1$ |
| $1$ | $1$ | $0$ |
Comme on peut le voir, cet opérateur renvoie toujours vrai sauf si $A$ et $B$ sont vrais en même temps. C'est en fait la négation du $et$, on la note $nand$ en anglais (pour $not\:and$)