k plus proches voisins
I. Présentation générale :¶
L'algorithme des "k plus proches voisins", "k neirest neighbours" en anglais ou KNN en abrégé, est très utilisé en apprentissage automatique, ou machine learning.
L'idée est assez simple :
- on considère une population d'individus de différentes catégories dont on a mesuré un ou plusieurs caractères
- on cherche à classer dans une catégorie un individu dont on ne connapit que la valeur des caractères
- pour ce faire on calculs la distance entre cet individu et l'ensemble des individus de la population connue
- on retient les k individus de la population les plus proches de notre inconnu
- on classe l'inconnu dansla catégorie la plus représentée parmi ces plus proches voisins.
L'illustration ci-dessous devrait clarifier les choses (source : https://en.wikipedia.org/wiki/K-nearest_neighbors_algorithm#/media/File:KnnClassification.svg) :
- La population connue est constituée de points bleux et rouges. Ce sont les deux catégories.
- Chaque point est caractérisé par son abscisse et son ordonnée
- On cherche à classer le point vert
- On calcule la distance entre le point vert et chacun des autres points
- Si l'on ne retient que les $3$ plus proches voisins alors notre inconnu sera classé parmi les "rouges"
- Si l'on retient les $5$ plus proches, il sera parmi les "bleus"
Comment calculer a distance ? Il existe plusieurs techniques possibles...
La plus classique est la distance euclidienne, c'est celle du cours de mathématiques :
- en deux dimensons : $$ d(A,B) = \sqrt{(x_A-x_B)^2+(y_A-y_B)^2}$$
- en $n$ dimensons (!) :
on pose $A\:(a_1,a_2,\dots,a_n)$ et $B\:(b_1,b_2,\dots,b_n)$ $$ d(A,B) = \sqrt{(a_1-b_1)^2+(a_2-b_2)^2 + \dots + (a_n-b_n)^2}$$
Ecrivons tout de suite notre fonction distance :
from math import sqrt
def distance(A, B) :
"""
Calcule la distance euclidienne entre deux points A et B présentés sous forme de listes de nombres
A et B sont des liste de nombres de même taille
Renvoie la distance euclidienne entre ces points
"""
assert len(A) == len(B), ValueError("Les points n'ont pas le même nombre de coordonnées (A : %s et B : %s)" % (len(A), len(B)))
somme = 0
for i in range(len(A)) :
somme += (A[i] - B[i])**2
return sqrt(somme)
# Essai avec deux coordonnées
distance([1,2],[4,3])
# Essai avec cinq coordonnées
distance([1,5,9,-8,4], [3,6,-9,-7,1])
II. Application :¶
L'exemple archi-classique de KNN avec python est celui-des iris (https://pixees.fr/informatiquelycee/n_site/nsi_prem_knn.html). Essayons-en un autre.
II.1 Prépration des données :¶
Nous allons utiliser des données de botaniques receuillies par Pedro F. B. Silva. Dans sa thès de 2013, ce chercheur a utilisé KNN afin de déterminer l'espèce d'une plante. Il a pour cela mesuré $14$ attributs sur chacune des $340$ feuilles prélevées parmi $40$ espèces.
Lire à ce propos le readMe.pdf dans le dossier leaf.
Importons les données :
import csv
csvfile = open ("./leaf/leaf.csv", "r")
lines = csv.reader(csvfile)
dataset = list (lines)
# On n'affiche que les 10 premières lignes
print(dataset[:10])
Organisons cela (en convertissant les données numériques au format souhaité):
# On convertit en réel
for ind in dataset:
ind[1] = int(ind[1])
for i in range (2,len(ind)):
ind[i] = float(ind[i])
print(dataset[0])
Pour les besoins ce ce cours, on extrait $3$ valeurs au hasard afin de constituer nos individus "mystères" :
from random import randint
individus_mysteres = []
for i in range(3) :
indice = randint(0, len(dataset)-1)
individus_mysteres.append(dataset.pop(indice))
print(individus_mysteres)
L'analyse en composante principale est une méthode statistique permettant de ramener un espace en $n$ dimensions (ici $14$) en un espace à $2$ dimensions sans perdre trop d'informations. Cela permet de visualiser nos données. Les couleurs correspondent aux espèces.
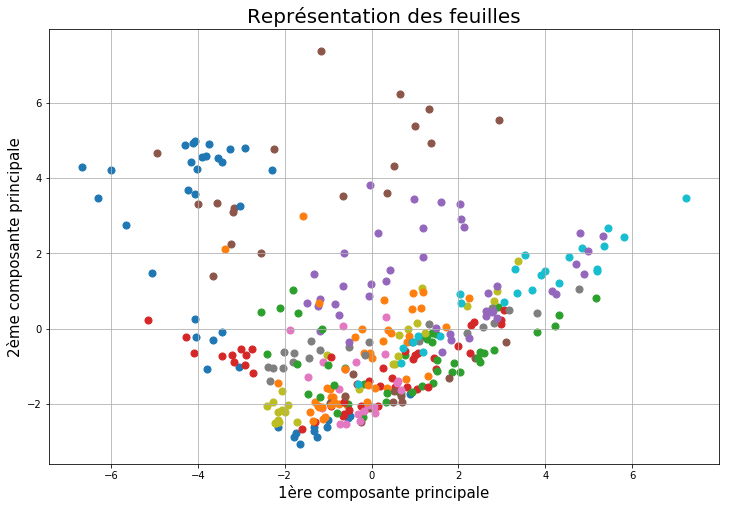
On se rend compte que des feuilles de la même espèce sont globalement dans la même région du graphique.
II.2 Traitement :¶
La méthode a été décrite plus haut : passons directement au code en python :
def knn(population, individu, k) :
"""
Classifie l'individu proposé dans l'une des catégorie représentée dans la liste population en fonction de ses k plus prhces voisins
population est une liste d'individus représentés des listes à n+2 valeurs
(la catégorie en chaîne de caractèr, le numéro de spécimen en entier et n coordonnées numériques )
individu est l'individu à classer. C'est une liste de n coordonnées numériques
k est le nombre de voisins à prendre en compte
Renvoie la catégorie dans laquelle on place l'individu
"""
# cette liste contient la distance de chaque individu
# de l'échantillon à l'individu inconnu et sa catégorie
liste_distances = []
for i in range(len(population)) :
liste_distances.append((distance(population[i][2:], individu), population[i][0]))
# tri du tableau selon les distances
liste_distances = sorted(liste_distances, key= lambda x : x[0])
#on retient les k premiers
k_plus_proches = []
for i in range(k) :
k_plus_proches.append(liste_distances[i][1])
# On compte les occurences de chaque catégorie parmi ces voisins à l'aide d'un dictonnaire
dico = {}
for n in k_plus_proches :
if n in dico.keys() :
dico[n] += 1
else :
dico[n] = 1
#On extrait la catégorie la plus représentée
categorie = max(dico.items(), key=lambda x: x[1])[0]
return categorie
On teste avec un individu mystère
knn(dataset, individus_mysteres[0][2:], 3)
On vérifie :
print(individus_mysteres[0][0])
Avec tous les individus mystères :
nb_erreurs = 0
for i in range(len(individus_mysteres)) :
prediction = knn(dataset, individus_mysteres[i][2:], 2)
print("Prédiction : %s // Attendu : %s" % (prediction, individus_mysteres[i][0]))
if prediction != individus_mysteres[i][0] :
nb_erreurs += 1
print("Pourcentage d'erreur : %s" % str(nb_erreurs/len(individus_mysteres)))
Et si l'on augmente le nombre de voisins pris en compte ?
nb_erreurs = 0
for i in range(len(individus_mysteres)) :
prediction = knn(dataset, individus_mysteres[i][2:], 5)
print("Prédiction : %s // Attendu : %s" % (prediction, individus_mysteres[i][0]))
if prediction != individus_mysteres[i][0] :
nb_erreurs += 1
print("Pourcentage d'erreur : %s" % str(nb_erreurs/len(individus_mysteres)))
