Un arbre est une structure de données permettant entre autres choses de décrire les relations hiérarchiques entre des objets.

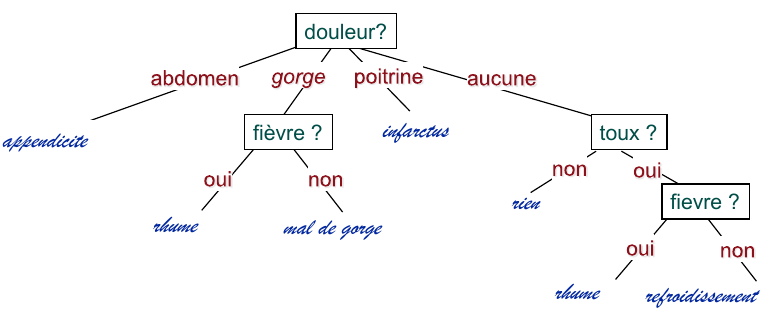
On peut par exemple les utiliser afin de représenter des arbres de décision.

I. Définitions

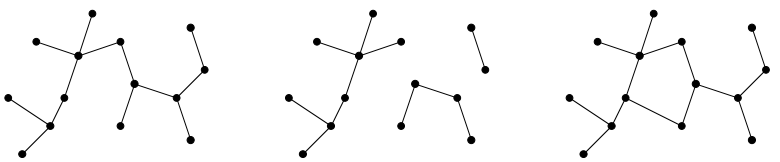
Un arbre est un type particulier de graphe. A ce titre, un arbre est constitué :

• de sommets : on parle ici de noeud
• d’arêtes : les liens entre les sommets

Un arbre est un graphe :

• non orienté : les arêtes ne comportent pas de direction, le lien allant d’un sommet père à un enfant est le même que celui allant de l’enfant au père
• connexe : aucun des sommets n’est isolé, tous font partie de l’arbre
• non cyclique : il est interdit d’avoir des boucles dans un arbre

Le vocabulaire associé est le suivant (entre parenthèse les traductions en anglais):

• la racine (root) est le sommet principal. C’est le seul à ne pas avoir de parent
• la profondeur (level) d’un noeud est sa position du noeud dans l’arbre. C’est la longueur du chemin entre la racine et le noeud
• la hauteur d’un arbre est sa profondeur maximale
• la taille d’un arbre est son nombre de noeud
• le parent (parent) d’un noeud est le noeud qui le précède directement dans l’arbre
• les ancêtres (ancestors) d’un noeud sont son parents et les parents de ses parents
• les enfants (children) d’un noeud sont les noeuds qui lui sont directement reliés au niveau supérieur
• les descendants d’un noeud sont ses enfants et les enfants de ses enfants
• des noeuds de même parent sont frères (siblings)
• un noeud sans enfant est situé en bas de l’arbre : c’est une feuille (leave)
• un noeud qui n’est pas une feuille est un noeud interieur
• des noeuds de même profondeur sont des voisins (neighbors)

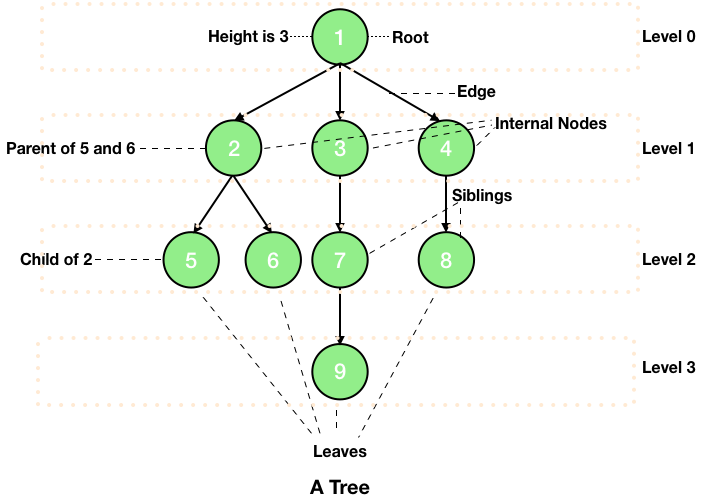
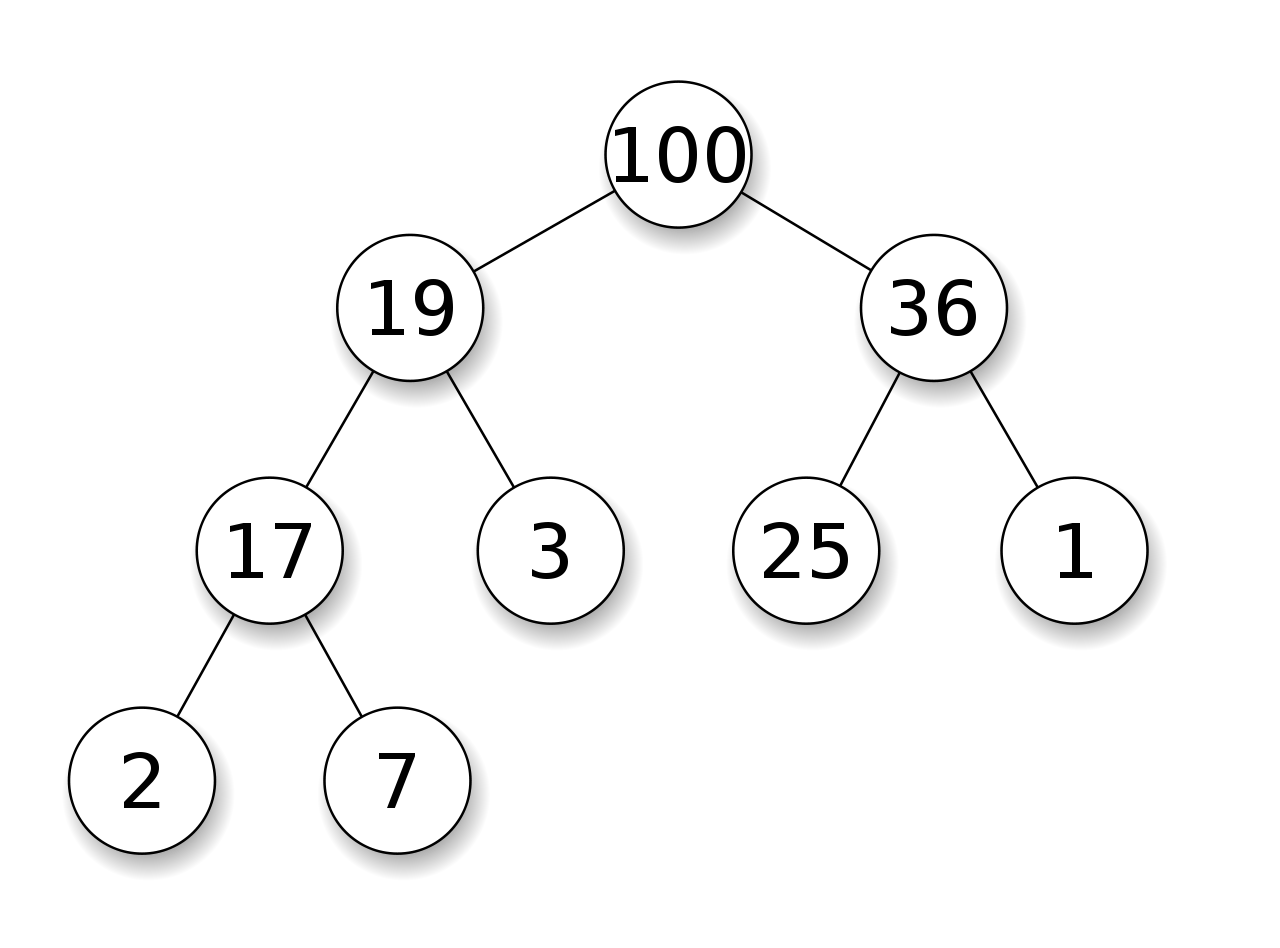
Un arbre binaire est un arbre tel que chaque noeud possède au maximum deux enfants. On parle alors de fils gauche et de fils droit.

II. Implémentation

Il existe plusieurs façon de représenter les arbres en informatique. L’une des méthode classique est de les définir de façon récursive comme des noeuds pointant vers d’autres noeuds.

La structure de base est alors le noeud. Celui-ci contient :

• un pointeur vers son parent (pas indispensable)
• des données. On les regroupe dans la clé
• si besoin, des pointeurs vers ses enfants

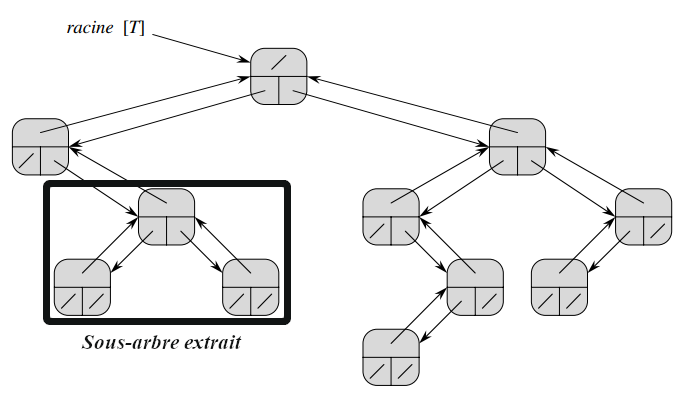
L’arbre est tant que tel ne contient alors qu’un seul attribut : sa racine.

Afin de créer un sous-arbre-extrait, on choisit un noeud et on crée un arbre en précisant qu’il est la racine.

III. Algorithmes

1. Hauteur de l’arbre

On peut calculer la hauteur d’un arbre en utilisant une fonction récursive (une fonction qui s’appelle elle-même). Le code ci-dessous correspond au cas de figure d’un arbre binaire.

hauteur(arbre)
    Si arbre est vide :
        Retourner 0
    Sinon :
        Retourner 1 + max(hauteur(Sous-arbre gauche), hauteur(Sous-arbre droit))

2. Taille de l’arbre

On rappelle que la taille d’un arbre est égale au nombre de noeuds non-vides qu’il contient. Là encore il est possible de déterminer la taille à l’aide d’une fonction récursive :

taille(arbre)
    Si arbre est vide :
        Retourner 0
    Sinon :
        Retourner 1 + taille(Sous-arbre gauche) + taille(Sous-arbre droit)

3. Parcours de l’arbre

Il est souvent utile de parcourir l’ensemble des noeuds d’un arbre, ne serait-ce que pour les compter par exemple. Le parcours peut aussi être utile afin de rechercher une valeur dans un arbre.

On distingue globalement deux méthodes de parcours :

• les parcours en largeur d’abord: on visite tous les noeuds d’une certaine profondeur avant de passer à la profondeur suivante
• les parcours en profondeur d’abord: on visite un noeud et tous les descendants avant de passer à ses voisins. Il en existe plusieurs

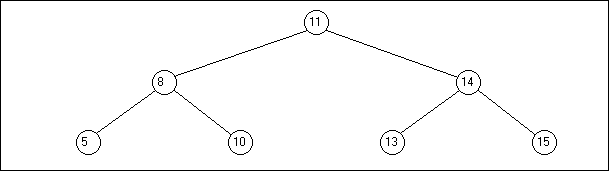
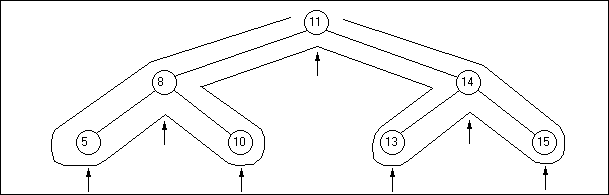
Sur la figure, le parcours en largeur donnera l’ordre suivant (on convient que les noeuds de gauche sont visités avant ceux de droite) :

\[11 \rightarrow 8 \rightarrow 14 \rightarrow 5 \rightarrow 10 \rightarrow 13 \rightarrow 15\]

Un parcours en profondeur pourra donner :

\[11 \rightarrow 8 \rightarrow 5 \rightarrow 10 \rightarrow 14 \rightarrow 13 \rightarrow 15\]

On peut implémenter un parcours en largeur à l’aide d’une file :

ParcoursLargeur(Graphe G):
    f est une file vide
    Enfiler la racine de G dans f
    Tant que la f est non vide
        Défiler un sommet s de f
        Afficher s
        Pour tout voisin v de s dans G
            Enfiler v dans f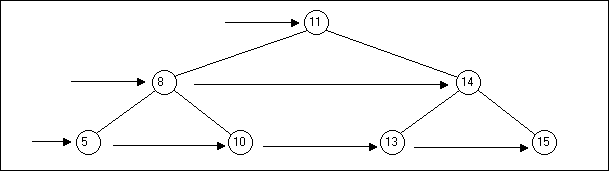

Les parcours en profondeur peuvent eux être définis de façon récursive. Afin de parcourir un arbre, on parcours successivement tous les sous-arbres extraits à partir des enfants de sa racine.On distingue :

• les parcours préfixe dans lesquels le noeud est traîter avant ses enfants
• et les parcours postfixe dans lequel il est traité ensuite

ParcoursPréfixe(Graphe G):
    Afficher la racine de G
    Pour tous les enfants e de la racine :
        ParcoursPréfixe( Sous-Arbre de racine e )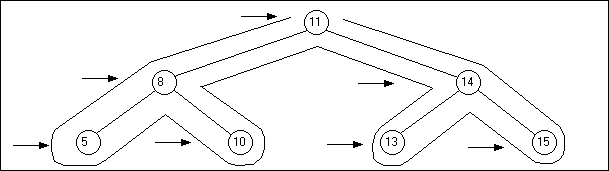

ParcoursPostfixe(Graphe G):
    Pour tous les enfants e de la racine :
        ParcoursPréfixe( Sous-Arbre de racine e )
    Afficher la racine de G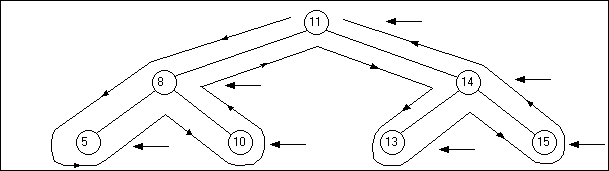

Remarque : dans le cas des arbres binaires (deux enfants au maximum), on peut définir le parcours infixe dans lequel on visite un noeud entre la visite de l’enfant gauche et celle du droit :

ParcoursInfixe(Graphe G):
    ParcoursPréfixe( Sous-Arbre gauche de la racine de G )
    Afficher la racine de G
    ParcoursPréfixe( Sous-Arbre droit de la racine de G )