Un arbre binaire de recherche (ABR) est un type aprticulier d’arbre permettant de rechercher très efficacement des valeurs dans un ensemble

I. Structure

1. Caractéristiques

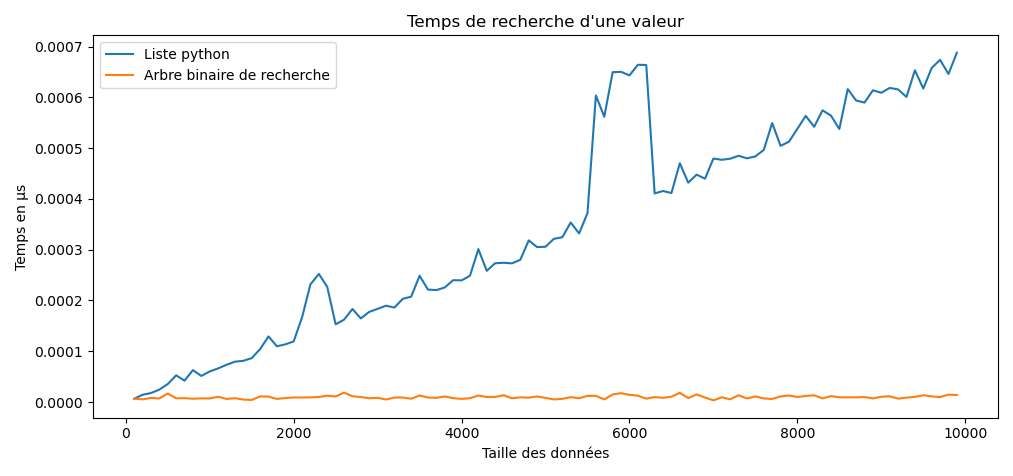
Voici un ABR :

Que remarque-t-on ?

• c’est un arbre (aucun noeud n’est isolé, il n’y a pas de cycle)
• chaque noeud possède au maximum deux enfants que l’on nomme communément gauche et droit
• à chaque noeud correspond une clé qui est d’un type comparable (que l’on peut trier, comme els nombres ou les chaînes de caractères)
• la clé du noeud de gauche est toujours inférieure ou égale à celle du parent
• la clé du noeud de droite est toujours supérieure ou égale à celle du parent

On comprend dès lors l’intérêt de cette structure : même si les données ne sont pas triées (la clé de la racine n’est pas la valeur minimale ou maximale en particulier), on ets assuré que le minimum des valeurs sera la clé de la feuille la plus à gauche ! A l’inverse, le maximum sera la clé de la feuille la plus à droite.

2. Hauteur en fonction de la taille

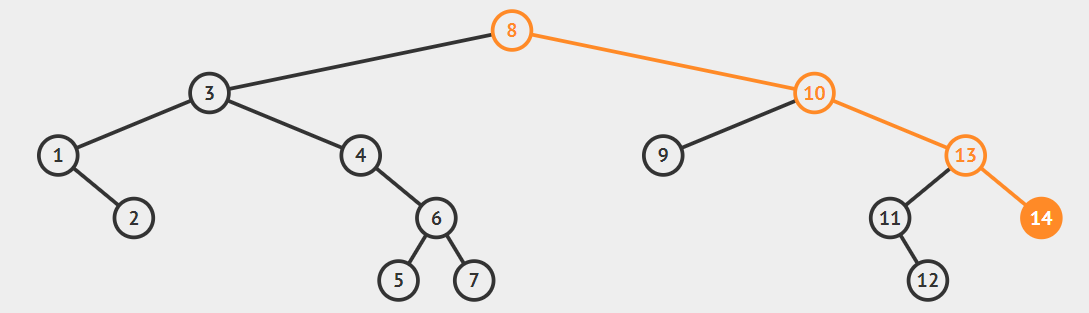
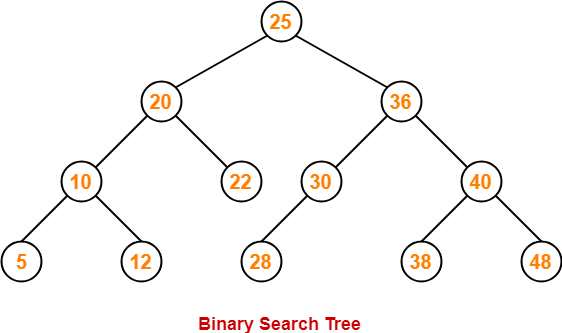
Quelle est la hauteur d’un ABR ? Imaginons que nous ayons \(1\,000\) valeurs à trier. Un arbre binaire à \(1\) niveau peut contenir un seul noeud, à \(2\) niveaux \(3\) noeuds, \(3\) niveaux \(7\) noeuds …

En fait un ABR à \(n\) niveaux peut contenir \(2^n-1\) noeuds au maximum.

Ainsi, pour placer \(1\,000\) valeurs il nous faudra au minimum \(10\) niveaux : en effet \(2^{10}-1 = 1\,023\).

On peut ainsi retenir la hauteur minimale d’un arbre de taille \(n\) vaut la partie entière de \(log_2(n)\), c’est à dire le plus petit entier \(p\) tel que \(2^p\) dépasse \(n\).

Ce calcul est valable si les données sont bien réparties dans l’arbre. A l’autre extrême, on peut imaginer que les données étaient triées lors de la création de l’arbre : on n’a fait que remplir les noeuds de droite ! Dans ce cas la hauteur vaudra \(n\).

3. Taille en fonction de la hauteur

Supponsons qu’un arbre binaire ait une hauteur de \(h\). Combien de noeuds peut-on placer à l’intérieur ?

Dans un arbre binaire à \(h\) niveaux, il y a au maximum \(2^{h-1}\) feuilles et en tout \(1+2+\dots+2^{h-1} = \frac{1-2^h}{1-2} = 2^h-1\) noeuds en utilisant la somme des termes d’une suite géométrique.

II. Implémentation

Un ABR peut être construit de façon récursive en utilsant des ABR contenant trois attributs :

• la clé (la valeur contenue)
• un lien vers le noeud fils de gauche (dont la clé est inférieure ou égale)
• un lien vers le noeud fils de droite (dont la clé est supérieure ou égale)

L’ABR est alors un arbre dont les fils gauche et droit sont aussi des arbres…

Dans le cadre de ce cours on mettra en oeuvre les méthodes suivantes :

• création(valeur) : retourne un ABR dont la clé vaut valeur et sans enfants. En mettant la clé à VIDE on crée un ABR vide
• estVide() : indique si l’arbre est vide (ne contient pas de clé)
• insertion(arbre, clé) : insère un nouveau noeud dans l’arbre à la première position convenable disponible
• rechercher(arbre, clé) : détermine si un noeud de l’arbre porte cette clé

Voici une implémentation possible d’un ABR:

créationArbre(valeur) :
    Retourne un arbre réduit à un noeud dont la clé vaut valeur et dont les fils gauche et droit sont vides

estVide(arbre) :
    Si la clé de l'arbre est VIDE :
        Retourne VRAI
    Sinon :
        Retourne FAUX

inserer(arbre, valeur) :
    Si estVide(arbre) :
        la clé de l'arbre prend la valeur valeur
        le fils gauche est désormais un arbre de clé VIDE
        le fils droit est désormais un arbre de clé VIDE
    Sinon :
        Si valeur <= clé de l'arbre :
            Si estVide(gauche) :
                gauche vaut désormais créationArbre(valeur)
            Sinon :
                inserer(gauche, valeur)
        Sinon :
            Si estVide(droit) :
                droite vaut désormais créationArbre(valeur)
            Sinon :
                inserer(droite, valeur)

rechercher(arbre, valeur) :
    Si estVide(arbre) :
        Retourner FAUX
    Sinon :
        Si la clé de l'arbre == valeur :
            Retourner VRAI
        Sinon :
            Si clé de l'arbre < valeur :
                Retourner rechercher(gauche, valeur)
            Sinon :
                Retourner rechercher(droite, valeur)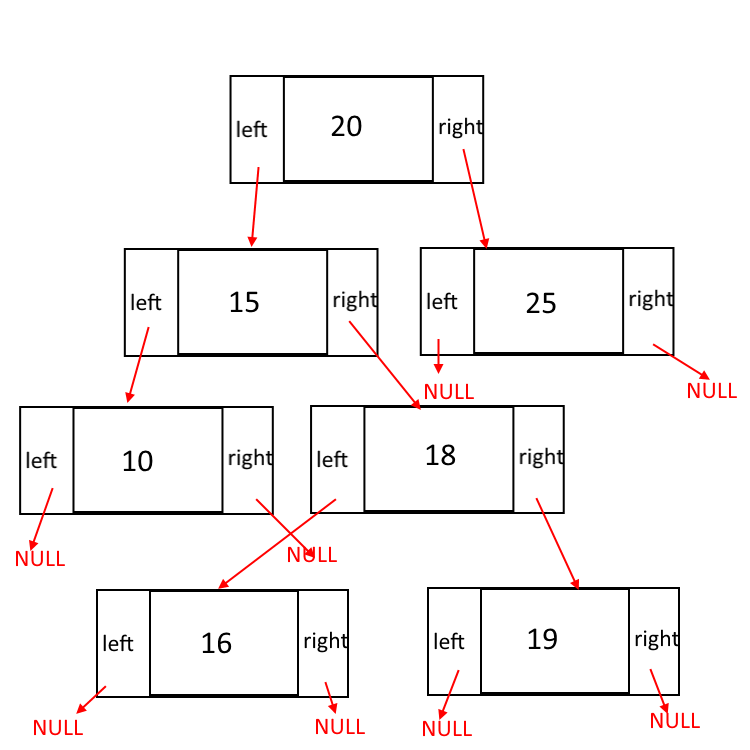

III. Intérêt

Les arbres binaires de recherches servent à chercher des éléments ! Il est donc intéressant de comparer leur complexité dans les opérations de recherches à celles d’autres structures de données.

Dans un tableau non ordonné, la recherche d’une clé nécessite au pire de lire toutes les valeurs : on ets en complexité linéraire \(O(n)\).

Dans un ABR, les clés étant triées à chaque étage, l’algorithme de recherche décide d’aller à gauhe ou à droite à chaque étape selon la valeur rencontrée. Il n’a donc pas à lire toutes les clés et fait au maximum \(h\) étapes, \(h\) étant la hauteur de l’arbre. Comme on a vu que \(h\) pouvait être calculé à partir de \(log_2(n)\), on est donc en complexité logarithmique (ce qui est meilleur qu’une complexité linéaire).