- Structure de données -
Les graphes
En 1929, le hongrois Frigyes Karinthy énonce l’hypothèse suivante : “Toute personne sur le globe peut en contacter une autre en s’addresseant à moins de six individus”. Dans les années 1960, le psychologue américane Stanley Milgram (celui de l’expérience) teste l’hypothèse : il fournit à des volontaires des courriers à faire suivre à une personne qu’ils ne connaissent pas vivant à 2500 km de chez elles et en ne les autorisant simplement à les faire passer à une personne de leur connaissance… La première lettre arriva après quatre jours. En comptant les intermédiaires il apparaut qu’en moyenne, les lettres étaient passées par 5 intermédiaires !

Ce nombre fut confirmé par des études plus récentes sur les réseaux sociaux…
Quel rapport avec un cours d’informatique ? Ces expériences portent sur les réseaux, sur le degré de connexion du réseau des communications humaines.
L’outil conceptuel permettant de modéliser ces objets est le graphe.
Un graphe est constitué de sommets et d’arêtes (nodes et vertex en anglais). Cet objet intervient autant dans la distibution de l’eau dans une ville (les sommets sont les bâtiments et les arêtes les tuyaux) que dans la modélisation d’internet (les ordinateurs et les câbles/liaisons sans-fils).
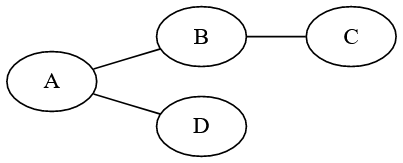
Dans le graphe de la figure 2, \(A\), \(B\), \(\dots\) sont des sommets, \((A,B)\), \((B,C)\) sont des arêtes.
Deux sommets sont adjacents, ou voisins, si une arête les relie. \(A\) et \(B\) sont adjacents mais pas \(A\) et \(E\).
Le degré d’un sommet est le nombre d’arête y arrivant. Ainsi le degré de \(A\) est \(3\), celui de \(D\) est \(4\)
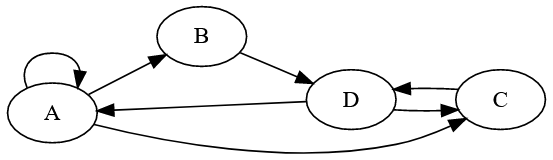
Un graphe peut être orienté ou non :
dans un graphe non orienté, l’arête \(A \rightarrow B\) est identique à l’arête \(B \rightarrow A\). Si \(A\) connaît \(B\) alors \(B\) connaît \(A\)
dans un graphe orienté, les arêtes peuvent différer : dans une ville, il peut exister un chemin allant de \(A\) vers \(B\) mais pas de \(B\) vers \(A\), il suffit d’avoir un sens interdit !
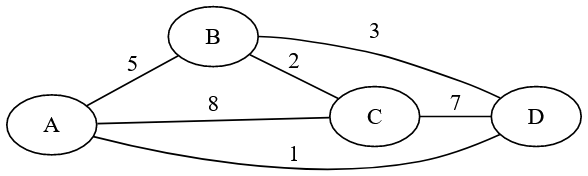
Un graphe peut être pondéré ou non. Dans un graphe pondéré, on associe un nombre, un poids, à chaque arête. Un grpahe permettant de déterminer le trajet le plus court entre deux sommets contient des informations sur la longueur des arêtes. Cette longueur peut être en kilomètres (on aura le chemin le plus court en distance) ou en minutes (on aura le trajet le plus court en temps).
On peut représenter informatiquement les graphes de deux façons classiques :
Dans cette implémentation, on se contente d’indiquer quels sommets sont reliés à quels autres à l’aide de listes. On peut par exemple utiliser des dictionnaires python.
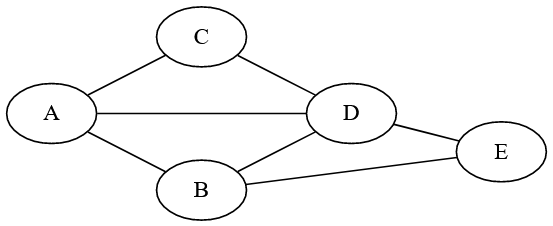
# Représentation du grpahe de la figure 2
# à l'aide d'une liste d'adjacence
graphe = {
"A" : ["B", "C", "D"],
"B" : ["A", "D", "E"],
"C" : ["A", "D"],
"D" : ["A", "B", "C", "E"],
"E" : ["B", "D"]
}Cette représentation facile à mettre en oeuvre est à privilégier lorsque le nombre d’arêtes est faible par rapport au nombre de sommets.
On peut grâce à cette implémentation facilement connaître le degré un sommet :
Dans cette représentation, on utilise une matrice (un tableau de nombres). Il faut au préalable numéroter les sommets : \(A\) sera le premier et correspondra à la première ligne/colonne, \(B\) sera le deuxième et correspondra à la deuxième ligne/colonne…

Au sein de la matrice on place des valeurs selon l’existence d’une arête entre le sommet de la ligne et celui de la colonne :
Si l’on doit stocker un graphe pondéré, il suffit de placer le poids d’une arête dans la matrice.
Par exemple pour le graphe de la figure 4 :
\[ \begin{pmatrix} 0 & 5 & 8 & 1 \\ 5 & 0 & 2 & 3 \\ 8 & 2 & 0 & 7 \\ 1 & 3 & 7 & 0 \\ \end{pmatrix} \]
En python, on utilisera une liste de liste :
Remarque : dans le cas d’un graphe non orienté, la matrice d’ajacence est symétrique par rapport à la diagonale
On retourve un algorithme proche de celui rencontré avec les arbres à cette différence qu’il faut ici garder trace des sommets déjà rencontrés afin de ne pas “tomber” dans un cycle.
Largeur(Graphe G, Sommet depart) :
f est une File vide
Enfiler depart dans f
Marquer depart comme visité
Tant que f est non vide :
Défiler le sommet s
Afficher s
Pour tous les voisins v de s dans G :
Si v n'a pas été visité
Enfiler v dans f
Marquer v comme visité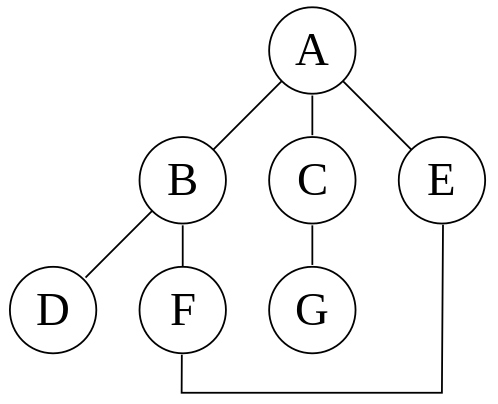
Dans le cas de la figure 6 et en partant de \(A\) on obtient : \(A \rightarrow B \rightarrow C \rightarrow E \rightarrow D \rightarrow F \rightarrow G\). \(F\) n’est visité qu’à la suite de \(B\) et pas après \(E\) car il a déjà été marqué.
Les parcours en largeur d’abord interviennent dans :
Pour le parcours en profondeur d’abord, on peut utiliser une fonction récursive :
Profondeur(graphe G, sommet depart) :
Marquer depart comme visité
Afficher depart
Pour tous les voisins v de depart
Si v n'a pas été visité :
Profondeur(G, t)Dans le cas du graphe de la figure 6 et en partant de \(A\) on obtient : \(A \rightarrow B \rightarrow D \rightarrow F \rightarrow E \rightarrow C \rightarrow G\)
Le parcours en profondeur d’abord intervient dans :
L’une des utilisations les plus courantes des graphes est la détermination de trajet : pour simplfifier, chaque coin de rue est un des sommets du graphe, les arêtes sont les rues. Le plus souvent on considère un graphe pondéré : à chaque rue on associe une longueur ou un temps de parcours.
L’algorithme le plus classique permettant de déterminer le chemin le plus court entre deux sommets est l’algorithme de Dijkstra.
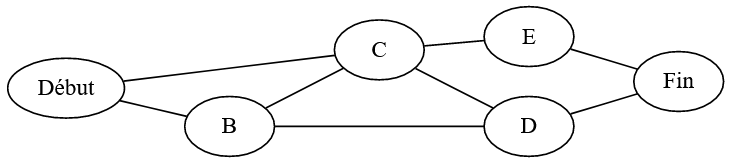
Simplifions le problème en considérant un graphe non pondéré. On ne cherche plus le chemin le plus court mais un chemin menant de \(Début\) à \(Fin\).
On peut utiliser alors l’algorithme (utilisant un parocurs en largeur) suivant :
Chemin(graphe G, sommet debut, sommet fin,chaîne chemin):
Ajouter debut à chemin (au sens de l'union : si debut est déjà dans le chemin on ne change rien,
s'il n'y est pas, on l'ajoute à la fin du chemin)
Si debut est égal à fin :
Retourner chemin
Pour tous les voisins v de debut dans G :
Si v n'est pas dans chemin :
nouveau_chemin = Chemin(G, v, fin, chemin)
Si nouveau_chemin est non Vide :
Retourner nouveau_chemin
Retourner VideDans le cas du graphe de la figure 9, on obtient :
| Etape | Sommet en cours | Voisins | Chemin en cours |
|---|---|---|---|
| 1 | \(Debut\) | \(B\), \(C\) | \(Debut\) |
| 2 | \(B\) | \(C\), \(D\) | \(Debut \rightarrow B\) |
| 3 | \(C\) | \(B\), \(D\), \(E\) | \(Debut \rightarrow B \rightarrow C\) |
| 4 | \(D\) | \(B\), \(C\), \(Fin\) | \(Debut \rightarrow B \rightarrow C \rightarrow D\) |
| 5 | \(Fin\) | \(D\), \(E\) | \(Debut \rightarrow B \rightarrow C \rightarrow D \rightarrow Fin\) |
On remarque que le chemin déterminé n’est pas le plus court… mais il est valide !
Imaginons que notre graphe représente des tâches à effectuer. Une arête entre deux tâches indique leur chronologie : l’arête \(A \rightarrow B\) indique que \(A\) doit être effectuée avant \(B\).
Que se passerait-il si un cycle \(A \rightarrow B \rightarrow C \rightarrow A\) existait dans le graphe ? Cela signifierait que \(B\) doit être effectué après \(A\), \(C\) après \(B\) et … \(A\) après \(C\) ! La chronologie des tâches serait incohérente…
Il est possible de déterminer l’existence de cycle dans un graphe en effectuant un parcours en profondeur. On prendra soin par contre de colorier les sommets en l’une de ces trois couleurs :
Initialement, tous les sommets sont blancs.
Cycle(graphe G, sommet depart) :
p est une Pile vide
Empiler depart sur p
Tant que p n'est pas vide :
Dépiler le sommet s
Pour tous les voisins blancs v de s dans G :
Si v est blanc :
Empiler v
Si s est noir :
Retouner VRAI
Sinon :
Colorier s en noir
Retourner FAUXAppliquons cet algorithme au graphe de la figure 7 en débutant avec le point \(A\).
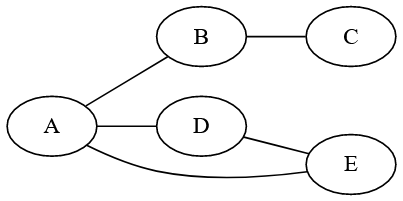
Et dans le cas où l’on a pas de cycle (figure 8) :