
- Langages et programmation -
Récursivité

Considérons les fonctions suivantes :
def A(n: int):
if n > 0:
print(f"A({n}) appelle B({n-1})")
retour = B(n-1)
print(f"A({n}) récupère la main")
return retour
else:
return f"A({n}) se termine"
def B(n: int):
if n > 0:
print(f"B({n}) appelle A({n-1})")
retour = A(n-1)
print(f"B({n}) récupère la main")
return retour
else :
print(f"B({n}) se termine")
return f"B({n}) s'est terminée"Que se passe-t’il lorsque l’on appelle A(5) ?
A(5) appelle B(4)
B(4) appelle A(3)
A(3) appelle B(2)
B(2) appelle A(1)
A(1) appelle B(0)
B(0) se termine
A(1) récupère la main
B(2) récupère la main
A(3) récupère la main
B(4) récupère la main
A(5) récupère la main
B(0) s'est terminéeLes appels successifs peuvent être visualisés sur le graphe de la figure 1.

Pourquoi s’arrête-t’on à l’appel de B(0) ? A cause du test if n > 0. Dès lors B termine son exécution en renvoyant B(0) s'est terminée à A(1) qui lui le transmet à B(2) etc…

En fait la bonne façon de décrire le fonctionnement de ces appels est un pile : lors des appels successifs, le système les empile sur la pile d’exécution. A chaque nouvel empilement, l’exécution d’une fonction est mise en attente jusqu’à ce qu’elle soit de nouveau en haut de la pile.
Lorsqu’une fonction se termine (avec un return), elle est dépilée et son résultat est transmis à la fonction qui l’avait appelée, fonction qui se retrouve alors au sommet de la pile et est exécutée….
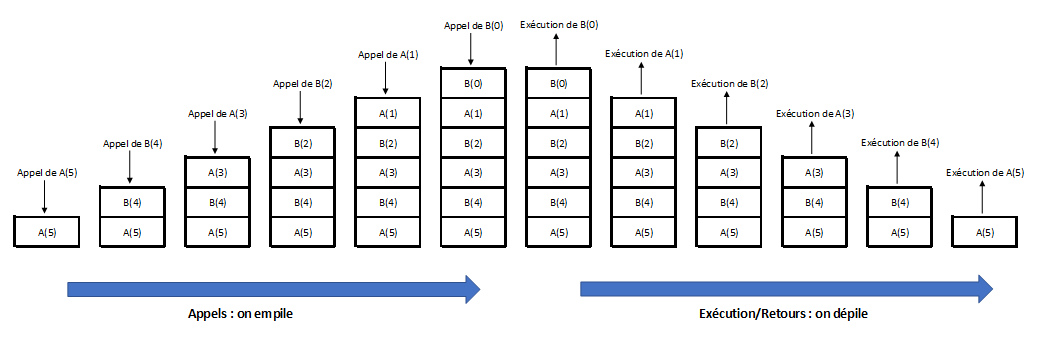
En dernière instance, la fonction A(5) récupère le résultat transmis par B(4), lui même obtenu de A(3)… C’est le Les dernières paroles de B renvoyé par A(0)
Maintenant que nous avons compris ce qu’est la pile d’exécution, nous pouvons étudier la fonction ci-dessous :
def inc(n: int):
if n == 5:
return f"On s'arrête à n={n}"
else:
print(f"n vaut {n}")
return inc(n+1)Que produit l’appel inc(0) ?
n vaut 0
n vaut 1
n vaut 2
n vaut 3
n vaut 4
"On s'arrête à n=5"Que se passe-t’il ? En fait la fonction s’appelle elle-même en augmentant (incrémentant) la valeur du paramètre de \(1\) à chaque fois. Lorsque n vaut \(5\), elle retourne sa valeur.
On peut construire le même schéma que ci-dessus :
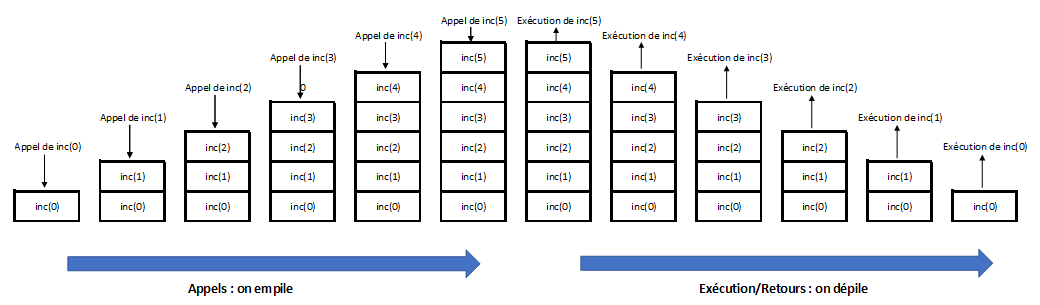
Que se passe-t’il si l’on appelle inc(6) ?
n vaut 6 n vaut 7 n vaut 8 n vaut 9 ... RecursionError: maximum recursion depth exceeded while calling a Python object
On obtient une erreur : en effet, notre fonction incrémente n jusqu’à ce qu’il soit égal à \(5\). Or en débutant à \(6\), on n’atteindra jamais la valeur \(5\) : le système empile donc des fonctions dans la pile d’exécution sans jamais dépiler : la pile déborde (stack overflow !). Une sécurité du langage permet de limiter ces cas de figure.
Remarque : Il ets possible de déterminer la profondeur limite de récursivité utilisé par python en utilisant sys.getrecursionlimit(). On peut la modifier en faisaint sys.setrecursionlimit().
Une fonction récursive est donc une fonction s’appelant elle-même.
Dans l’exemple de la première partie les fonctions A et B s’appelaient l’une l’autre : on parle alors de récursivité croisée.
Une fonction récursive doit gérer au minimum deux cas de figure :
Recursive(profondeur) :
Si "condition limite" :
Retourne le résultat
Sinon :
Retourne Recursive(profondeur + 1)Un exemple archi-classique de fonction récursive est le calcul de la factorielle d’un nombre entier positif. On rappelle que si \(n\) est un entier naturel non nul, alors sa factorielle est égale à \(n\,! = n \times (n-1) \times (n-2) \times \dots \times 2 \times 1\). Ainsi \(3\,! = 3 \times 2 \times 1 = 6\) et \(4\,! = 4 \times 3 \times 2 \times 1 = 24\). On remarque que \(4\,! = 4 \times 3\,!\) et de façon générale \(n\,! = n \times (n-1)\,!\).
On procède donc ainsi :
fact(n) :
Si n est égal à 1 :
# Cas de base
Retourner 1
Sinon :
# Cas général
Retourner n * fact(n-1)En python :

On retourve des fonctions récursives dans les cas suivants :

