Nos ordinateurs sont très rapides, nous les utilisons tous les jours, parfois trop sous la forme de nos smartphones. Ils peuvent même, parfois, nous sembler intelligents !

Sont-ils vraiment capables de tout faire ? Dans la mesure où ils manipulent des nombres, sont-il capables de tout calculer ? Répondre à cette question nécessite de s’intéresser à la calculabilité des fonctions informatiques.

Identifier les problèmes qu’un ordinateur est effectivement capable de résoudre, revient à s’intéresser à leur décidabilité.

I. Les programmes sont des nombres comme les autres…

Prenons un programme python simple :

print("Hello World")

Et son presque jumeau :

print("Hello world")

Ces “programmes” sont sauvés dans la mémoire sous le nom de hello1.py et hello2.py. Ces sauvegardes sont faites sous formes de bits, de 0 et de 1, en utilisant en l’occurence le codage ASCII. Le code ci-dessous permet de récupérer les nombres enregistrés sur le disque dur :

resultat = ""

with open("hello1.py", "rb") as f: # on ouvre le fichier
    while True: # Boucle infinie (on en sort avec le break !)
        octet = f.read(1)  # on lit un octet à la fois
        if octet == b'': # l'octet est vide, on a fini de lire le fichier => on quitte
            break  
        else : # l'octet est non vide : on le convertit en entier et on l'ajoute à resultat
            resultat += str(int.from_bytes(octet, byteorder='big')) + "-" 

print(resultat[:-1])

Qu’obtient-on avec hello1.py ?

112-114-105-110-116-40-34-72-101-108-108-111-32-87-111-114-108-100-34-41

Et avec hello2.py ?

112-114-105-110-116-40-34-72-101-108-108-111-32-119-111-114-108-100-34-41

Il y a bien une différence (le 87 = W du premer programme est remplacé par 119 = w dans le second).

On a ici affiché tous les octets sous forme d’entiers distincts afin de faciliter la lecture, on aurait pu aussi afficher tous les bits à la suite. Pour le premier programme cela donnerait :

11100001110010110100111011101110100...001

ce qui, converti en décimal donne : \(38\,416\,887\,839\,235\,554\,319\,162\,749\,993\,487\,037\,778\,089\)… C’est un grand nombre certes mais c’est un nombre ! Et encore, notre “pogramme” est plutôt simple (print("Hello World))…

L’idée à retenir est qu’un programme, stocké sur l’ordinateur, peut être interprété comme un nombre et donc un programme est une donnée comme une autre.

Remarque : Nous programme de conversion peut aussi se lire lui-même ! Dans ce cas là il renvoit \(165\dots874\), un nombre à \(1\,425\) chiffres !!

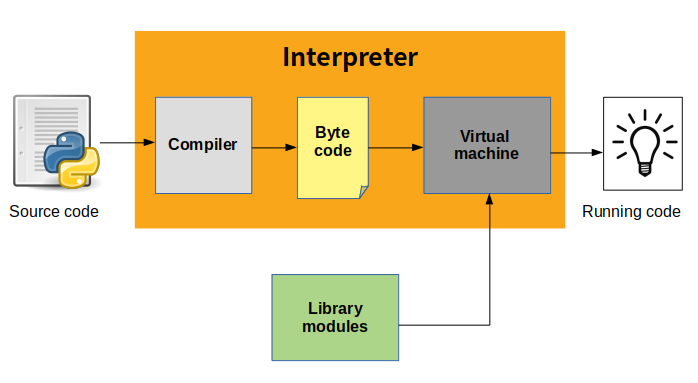
Cette opération de lecture du programme comme une donnée peut sembler alambiquée, inutile, mais en fait elle est réalisée à chaque fois que l’on exécute un code python. En effet, le fichier .py n’est pas exécuté directement par le processeur, il est compilé, traduit en instructions élémentaires, le bytecode, qui sera lui-même pris en argument par la machine virtuelle python qui le traduira pour qu’il soit exécuté par le(s) processeur(s) : un programme est une donnée !

II. Les machines de Turing

Pendant la première moitié du XX-ième siècle, les mathématiciens repensent les bases de leur science. David Hilbert (1862 - 1943) pose ainsi en 1928 la question de savoir s’il peut exister un algorithme capable pour chaque affirmation de juger si elle est vraie ou non. Il s’agit du Entscheidungsproblem, le problème de la décision.

Deux mathématiciens (logiciens, informaticiens… il est difficile de circonscrire leur travaux respectifs), Alonzo Church (1903 - 1995) et Alan Turing (1912 - 1954) prouvent indépendamment en 1936 qu’un tel algorihtme ne peut pas exister. Dans sa preuve, Turing présente sa fameuse machine de Turing qui n’est rien de moins que le modèle théorique de l’ordinateur.

La machine de Turing est constituée :

• d’un bandeau de longueur infinie (ce qui limite d’emblée sa réalisation pratique…) divisé en cellules
• d’une tête de lecture/écriture pouvant lire ou écrire une valeur dans une cellule
• d’un moteur capable de décaler la bande d’une cellule vers la gauche ou la droite

A ces éléments pratiques, on ajoute :

• un ensemble de caractères, que l’on appelle alphabet, que l’on a le droit d’écrire sur la bande (par exemple 0, 1 et le symbole vide _)
• un ensemble d’états dans lequel peut se trouver la machine (notés souvent \(q_1\) … \(q_n\))
• des règles de transitions du type :
  • si on est dans l’état \(q_3\) et que l’on lit 1 dans la cellule alors on écrit 0 à la place, on décale la bande vers la droite (d’un pas) et on passe dans l’état \(q_4\)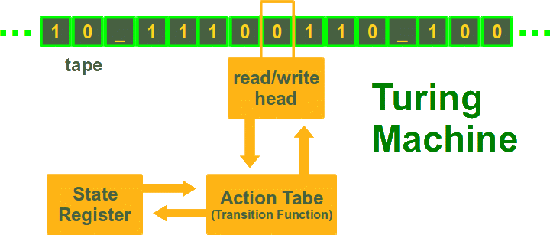

On retrouve le modèle d’un ordinateur :

• le bandeau joue le rôle de la mémoire
• la tête de lecture écriture est le processeur
• les règles de transition correspondent au programme

Il reste tout de même un problème : dans cette description, une machine est associée à un alphabet, un ensemble de règles de transitions… La machine qui multiplie un nombre par deux est complètement différente de celle qui multiplie par trois ! Turing fait un pas supplémentaire : il imagine une machine universelle qui réserve une place sur son bandeau pour encoder la description d’une autre machine : son alphabet, ses règles de transitions… Une machine de Turing (un programme) peut ainsi être une donnée pour une autre machine à l’image des programmes de notre ordinateur qui sont des données pour le compialteur ou le système d’exploitation. L’ordinateur est né.

Malgré sa simplicité, une machine de Turing est capable de faire fonctionner tous les algorithmes imaginables. La thèse de Church postule même que tout calcul réalisable concrètement par un être humain est réalisable par une machine de Turing. Un ordinateur peut donc calculer tout ce que peut calculer un être humain.

III. Décidabilité et problème de l’arrêt

On l’a vu, la machine de Turing a été présentée afin de répondre au problème de la décision (existe-t-il un algorithme capable de juger de la validité de n’importe quelle affirmation ?).

De façon plus générale, on dit qu’un problème informatique est décidable s’il est possible de fournir un algorithme capable d’y répondre (par oui ou non) quelle que soit l’entrée proposée. Le problème de la parité par exemple (“un nombre entier \(n\) donné est-il pair ?”) est décidable : l’algorithme testant la valeur du reste de \(n\) par \(2\) permet de répondre à la question.

Turing a reformulé la question générale du problème de la décision : existe-t-il un machine de Turing capable de juger qu’une autre machine, lorsqu’on lui donne une entrée précise, va fournir un résultat ou tomber dans une boucle infinie ? Existe-t-il donc un programme informatique capable de juger tous les autres programmes informatiques (en terme d’arrêt/boucle infinie). On parle en anglais de halting problem.

Turing fait une démonstration par l’absurde : il suppose qu’une telle machine existe et en déroulant son raisonnement de façon correcte finit par arriver à une absurdité. L’ensemble du raisonnement étant valide, l’erreur provenait de l’hypothèse de départ.

Voici une version très simplifiée de sa preuve :

• Turing fait l’hypothèse que la machine capable de juger de l’arrêt de toutes les autres machines existe. On l’appelle la \(Halting\,Machine\)
• Il construit alors une seconde machine \(B\) comme sur la figure : \(B\) contient la \(Halting\,Machine\) mais en modifie les sorties :
  • si le programme fourni en argument s’arrête, la machine \(B\) tombera dans une boucle infinie
  • si le programme ne s’arrête jamais (la \(Halting\,Machine\) le détecte comme tel), la machine \(B\) renvoie un résultat quelconque (NO sur la figure)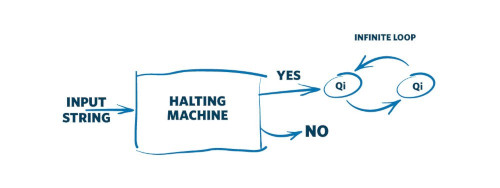

A partir de là, le raisonnement devient retors : Turing imagine que l’on fournit le code de la machine \(B\) à la machine \(B\) ! C’ets possible car une machine, un programme, est interprétable comme un nombre, comme une donnée. Que va dire la machine \(B\) d’elle-même ?

Si la \(Halting\,Machine\) juge que \(B\) s’arrête, on tombe dans la boucle infinie et \(B\) ne s’arrête pas… C’est incohérent.

Si la \(Halting\,Machine\) juge que \(B\) ne s’arrête pas, la machine \(B\) renvoie NO et … s’arrête !

Remarque : on reconnaît le classique paradoxe du menteur

Dans les deux cas on arrive à une absurdité… Où était le problème ? Dans l’hypothèse de l’existence de la \(Halting\,Machine\). Le problème de l’arrêt est donc indécidable.

De façon plus générale : il existe de problème qu’un ordinateur est incapable de résoudre. Nos ordinateurs comptent certes très vite mais ils ne peuvent pas tout faire…