Certains problèmes algorithmiques de grande taille peuvent être résolus à l’aide de sous-problèmes : si l’on souhaite par exemple déterminer le minimum d’une liste de nombres, on peut commencer par chercher les minimums de la partie gauche de la liste et celui de la partie droite puis comparer les deux. Le minimum général sera le plus petits des deux minimums.

Cette méthode est appelée Diviser Pour Régner. L’expression est attribuée à Philippe II de Macédoine, le père d’Alexandre le Grand. Il fallait alors l’entendre dans un sens politique.

I. Présentation générale

On considère un problème dont l’entrée est de taille importante. La méthode diviser pour régner (divide and conquer en anglais) consiste en trois étapes :

1. Partager le problème en sous-problèmes de taille inférieure (divisier)
2. Résoudre les sous-problèmes (régner)
3. Combiner leurs solutions afin de résoudre le problème de départ (combiner)

Bien souvent dans cette démarche on travaille récursivement : chaque sous-problème est lui aussi divisé en sous-problèmes de taille inférieure. On continue la division jusqu’à ce que le sous-problème ait une taille suffisante pour le résoudre facilement (c’est le cas de base de la récursion).

Imaginons par exemple un algorithme dans lequel on peut partager le problème en trois sous-problème de taille \(\frac{n}{3}\) pour lequel le cas de base nécessite des problèmes de taille \(2\). Si l’on part d’un problème de taille \(18\), on résout le problème comme sur la figure 3.

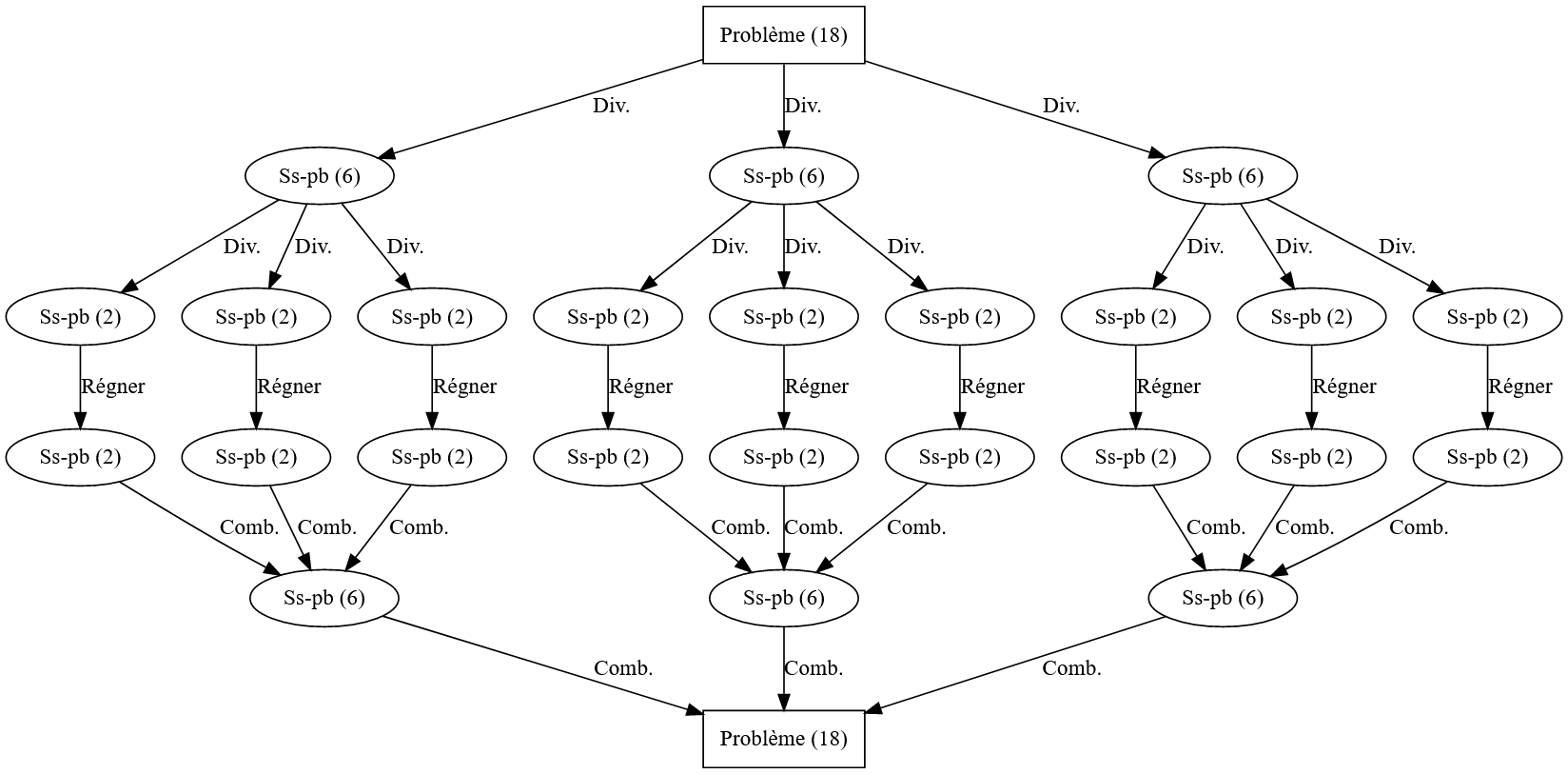
La méthode est particulièrement efficace si la combinaison des sous-problèmes simplifie les calculs. Par exemple si l’on partage un problème de taille \(n\) en \(2\) sous-problèmes de taile \(\frac{n}{2}\) mais que leur résolution puis leur combinaison amène à faire pour chacun \(\frac{n}{2}\) calculs, le bilan est nul en termes de complexité (\(2 \times \frac{n}{2} = n\)).

Si par contre les sous-problèmes sont plus faciles à résoudre ou si leur combinaison permet des économies de calculs, on y gagne : dans le cas précédent, si les sous-problèmes nécessitent \(\frac{n}{3}\) opérations, le bilan est intéressant : \(2\times \frac{n}{3} = \frac{2}{3} n < n\).

II. Le tri fusion

Une application classique de la méthode Diviser pour régner est le tri fusion. On rappelle tout d’abord que l’on a étudié en Première les tris par sélection (on sélectionne à chaque étape le plus petit élément restant à trier) et par insertion (on décale les valeurs vers le début de la liste jusqu’à ce qu’elles soient en position). Ces deux méthodes sont en complexité \(O(n^2)\).

Le tri fusion fonctionne ainsi (on fait l’hypothèse que la taille du tableau \(n\) est une puissance de \(2\) afin d’alléger les notations mais la méthode fonctionne aussi pour des tailles quelconques) :

• on considère un tableau de taille \(n\)
• on le partage en deux sous-tableaux de taille \(\frac{n}{2}\)
• on partage récursivement chaque sous-tableau en \(2\) jusqu’à obtenir des tableaux de taille \(1\) (étape diviser)
• on trie ces tableaux de taille \(1\) (cette étape régner est facile, un tableau d’un seul élément est toujours trié !)
• on fusionne les tableaux de tailles \(1\) en des tableaux de taille \(2\) (étape combiner)
• on fusionne les sous-tableaux en tableaux deux fois plus grands (étape combiner)

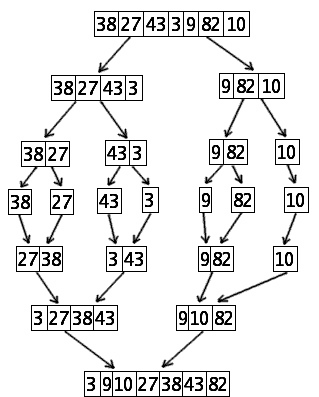
Le code de l’agorithme peut être construit autour de deux fonctions :

• la fonction fusion qui fusionne les tableaux lors de leur combinaison
• la fonction tri_fusion, fonction récursive qui fait l’ensemble de la démarche

On choisit de proposer une version du tri non en-place (qui utilise des tableaux annexes) afin de simplifier le code.

Voici la fonction fusion :

fusion(tableau A, tableau B) :
  R est un tableau vide
  
  Tant que A est non-vide et B est non-vide :
    Si A[0] est inférieur ou égal à B[0] :
      Ajouter A[0] à la fin de C
      Retirer A[0] de A
    Sinon :
      Ajouter B[0] à la fin de C
      Retirer B[0] de B
  
  Tant que A est non vide :
    Ajouter A[0] à la fin de C
    Retirer A[0] de A
  
  Tant que B est non vide :
    Ajouter B[0] à la fin de C
    Retirer B[0] de B
  
  Renvoyer C

On commence par créer un tableau C vide que l’on complète avec les plus petits éléments de A et B (qui sont déjà triés) tant que les deux tableaux sont non-vides. Dès que l’un des tableaux est vide, on termine en vidant l’autre dans C. On remarque que cette fonction est construite autour de boucles Pour effectuant autant d’itérations qu’il y a de valeurs dans le plus long des tableaux A ou B. Si les tableaux sont de taille \(n\) on est donc en complexité \(O(n)\).

La fonction tri_fusion quant à elle fonctionne ainsi :

tri_fusion(A) :
  Si A est longueur 1 :
    Renvoyer A
  Sinon :
    milieu prend la valeur (longueur de A)// 2 # le double // est la division entière
    
    A_gauche prend la valeur tri_fusion(A[0..(milieu-1)])
    A_droite prend la valeur tri_fusion(A[milieu..fin])
    
    Renvoyer fusion(A_gauche, A_droite)

Quelle est la complexité de cette méthode ? Supposons que le tableau de départ soit de taille \(32\) (une puissance de \(2\) à nouveau afin de simplifier les choses). Les différentes découpent créent des tableaux de tailles \(32 \rightarrow 16 \rightarrow 8 \rightarrow 4 \rightarrow 2 \rightarrow 1\). Il en faut \(5\) car \(32 = 2^5\).

De façon générale pour un tableau de taille \(n\) il faut \(\log_2(n)\) découpes afin d’arriver à des sous-tableaux de taille \(1\).

Comment trier ces tableaux de taille \(1\) ? Ils le sont déjà et comme il y en a \(n\), \(1\) par valeur du tableau de départ, l’étape \(régner\) est de complexité \(O(n)\).

Observons ensuite la figure 5.

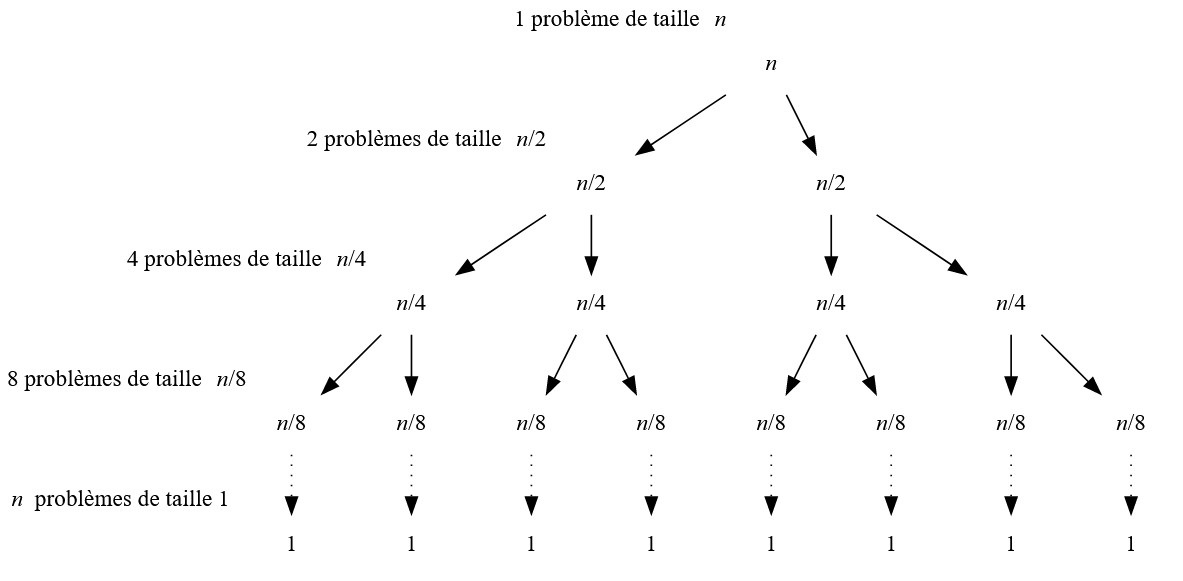
A chaque étape, on doit fusionner les tableaux du niveau inférieur afin de créer le tableau supérieur. Si les sous-tableaux sont de taille \(\frac{n}{4}\) par exemple, il y en a alors \(4\), il faudra \(4\) fusions de complexité \(\frac{n}{4}\). Cette étape sera donc de complexité \(O(4 \times \frac{n}{4} = n)\).

On peut ainsi montrer que chaque étape de fusion (les combinaison) est de complexité \(O(n)\).

Donc chacun des niveaux de la figure 5 est de complexité \(O(n)\). Or il y a \(\log_2(n)\) niveaux : la complexité totale de l’algorithme de tri-fusion est donc de \(O(n \log_2(n))\).

La fonction \(n \mapsto \log_2(n)\) croît au départ plus rapidement que \(n \mapsto \log_2(n)\) mais voit son rythme “ralentir” pour finir par évoluer plus lentement : le tri-fusion devient avantageux pour des tableaux de grandes tailles.

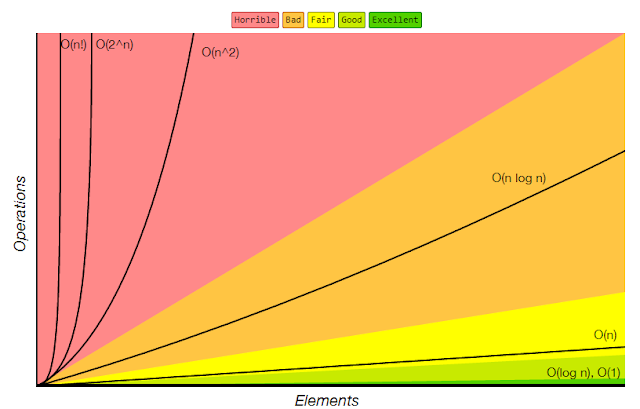
Reste toutefois le problème de l’espace mémoire réservé si l’on procède comme indiqué plus haut : on a créé beaucoup de tableaux intermédiaires ce qui peut poser soucis si l’espace mémoire est limité.