Bien souvent, le nombre de calculs nécessaires à la résolution d’un problème augmente rapidement avec la taille du problème (comme pour le voyageur de commerce). Dans certains cas toutefois, il est possible de résoudre un grand problème en résolvant plusieurs problèmes de taille inférieure. C’est l’approche que l’on peut retrouver dans la méthode “diviser pour régner”.

La programmation dynamique utilise cette approche en gardant trace toutefois des solutions aux sous-problèmes déjà résolus afin de les réutiliser.

I. Première approche avec la suite de Fibonacci

Au XIII-ième siècle, Léonard de Pise dit Fibonacci pose le problème récréatif suivant :

• on se donne un couple de lapins juvéniles
• après deux mois, ce couple engendre un nouveau couple de lapins
• tous les couples se reproduisent à partir du troisième mois suivant leur naissance et engendre alors un couple par mois
• combien de couples y-aura-t’il après \(n\) mois ?

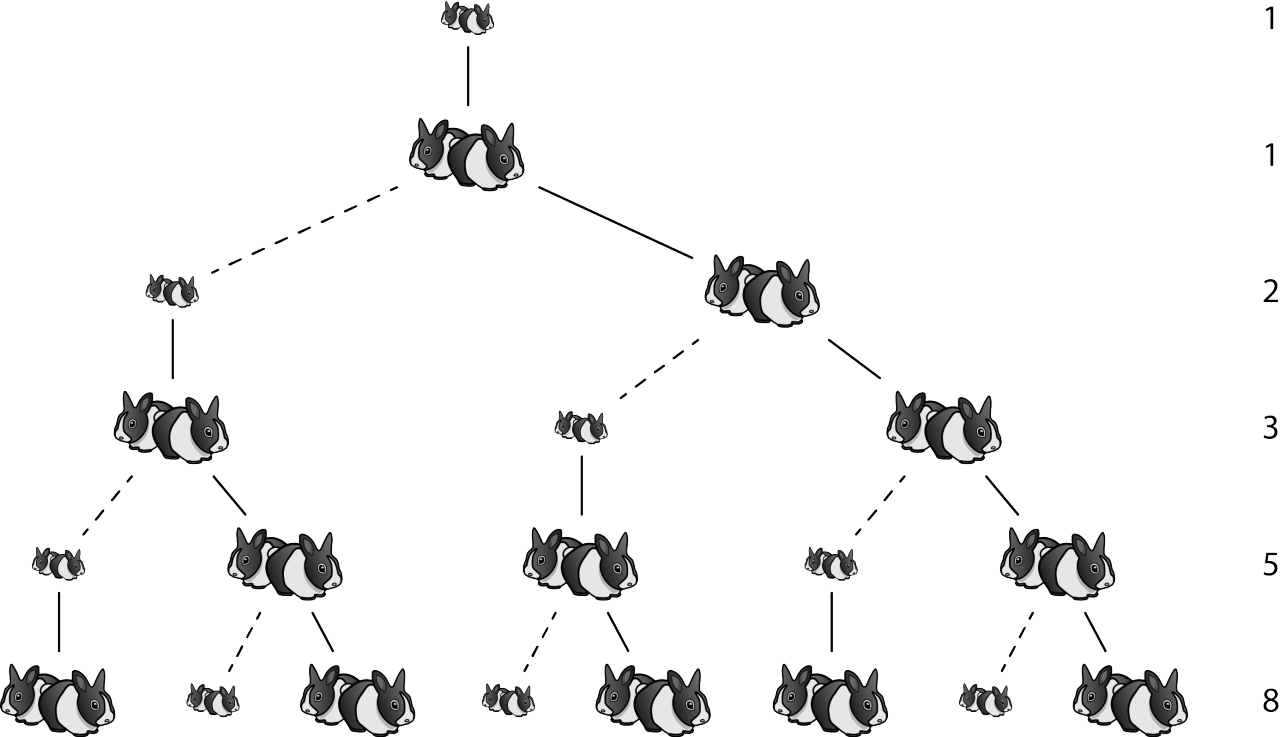
Cette énigme amène à considérer la suite \((F_n)\) suivante :

\[F_0 = 0\] \[F_1 = 1\] \[\forall n >= 2,\,F_n=F_{n-1}+F_{n-2}\]

On obient alors la suite suivante :

\[F_0 = 0 \rightarrow F_1=1 \rightarrow F_2=1 \rightarrow F_3=2 \rightarrow F_4=3 \rightarrow F_5=5 \rightarrow \dots\]

Le calcul des termes de cette suite peut se faire facilement à l’aide d’un programme récursif :

def fibonacci_recursif(n):
    if n <= 1:
        return n
    else:
        return fibonacci_recursif(n-1) + fibonacci_recursif(n-2)

Cette méthode présente toutefois un gros problème. Mettons que l’on souhaite calculer \(F_{10}\). Ce calcul aura besoin de \(F_9\) et de \(F_8\). Mais la valeur de \(F_9\) nécessitera aussi \(F_8\). Le programme proposé plus haut recalculera cette valeur sans se soucier du fait qu’elle ait déjà été déterminée… A vrai dire, le calcul de \(F_{10}\) par cette méthode nécessite \(177\) appels à la fonction fibonnacci_recursif alors que \(8\) calculs devraient suffire (ceux de \(F_2\) à \(F_{10}\)) ! Le calcul de \(F_{40}\) nécessite \(331\,160\,281\) appels là où \(38\) calculs devraient suffire…

Comment faire mieux ? Il suffirait de garder la trace des termes de la suite déjà calculés. Mettons que l’on souhaite calculer \(F_{n}\):

• s’il a déjà été calculé et sauvé dans un tableau F, on renvoie la valeur directement
• s’il n’a pas été déjà calculé :
  • si \(n\) vaut \(0\) ou \(1\), on retourne \(n\) (car \(F_0=0\) et \(F_1=1\))
  • sinon, on calcule la valeur de \(F_n\) en appelant la fonction récursivement

On s’est donc prémunis des calculs redondants en s’assurant que la valeur est connue ou non. L’algorithme est le suivant :

F est un tableau de n+1 nombres
Pour tout i allant de 0 à n :
  F[i] = -1

fibonnacci_dynamique(n) :
  Si F[n] vaut -1:
        Si n est inférieur ou égal à 1:
            F[n] prend la valeur n
        Sinon :
            F[n] prend la valeur fibonacci_dynamique(n-1) + fibonacci_dynamique(n-2)
  Renvoyer F[n]

Cette approche permet de calculer \(F_{10}\) en ne faisant que \(19\) appels (on rappelle qu’une valeur se calcule à partir des deux précédentes et \(19 \approx 2 \times 10\)).

Qu’avons nous fait ?

• On a découpé un problème compliqué en sous-problèmes
• On a calculé récursivement les solutions de ces sous-problèmes en gardant la trace des résultats obtenus
• On a combiné ces résultats afin de résoudre le problème principal

Cette approche est celle de la programmation dynamique développée par Richard Bellman dans les années 1950 :

1. on considère un problème d’optimisation (la détermination de la meilleur solution à un problème)
2. on découpe ce problème en sous-problèmes dont on cherche la solution optimale. Il faut être sûre que la solution optimale au problème de départ fait intervenir la solution optimale d’un des sous-problèmes traités (principe d’optimalité)
3. les sous-problèmes sont interdépendants : on les résout en gardant trace des solutions intermédiaires afin d’éviter les répétitions
4. on combine ces solutions afin de résoudre le problème initial

Le procédé permettant de garder trace des calculs intermédiaires s’appelle la mémoisation (il n’y a pas de “r”, ce n’est pas une faute d’ortographe).

Le lien entre les solutions des sous-problèmes et celle du problème de taille supérieure fait intervenir une relation de récurrence. Dans le cas de la suite de Fibonacci, c’est la relation \(F_n=F_{n-1}+F_{n-2}\).

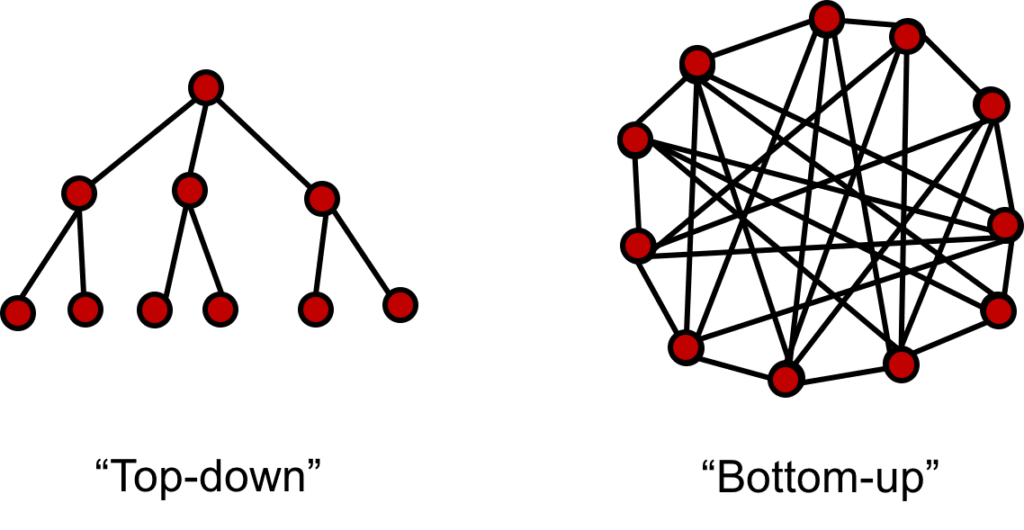
On a déterminé les valeurs de termes ici en débutant avec la valeur finale et en descendant. On parle d’approche Top-Down. Il serait aussi possible de résoudre ce problème en partant des valeurs de base (\(F_0\) et \(F_1\)) et en progressant de proche en proche jusqu’à obtenir la valeur cherchée \(F_n\). Cette approche ascendante (ou Bottom-Up) n’est toutefois pas toujours optimale car dans bien des cas il n’est pas nécessaire de calculer toutes les valeurs intermédiaires (c’est-à-dire de résoudre tous les problèmes de taille inférieure à celui cherché).

II. Rendu de monnaie optimal

Le problème du rendu de monnaie est classique en algorithmique : on se donne une caisse comportant des pièces de valeurs en euros données \(d_1\), \(d_2\), …, \(d_k\) (de valeurs croissantes \(d_i < d_{i+1}\)) et on souhaite rendre la somme de \(n\) euros.

Afin de s’assurer que le problème a toujours une solution on suppose :

• que la plus petite pièce vaut \(1\) (\(d_1=1\))
• que l’on possède une infinité de pièces de chaque catégorie

On rajoute ici la contrainte de rendre un minimum de pièces.

Un algorithme glouton n’est pas idéal ici. Si l’on considère par exemple des “pièces” de \(1\), \(10\) et \(25\) et que l’on souhaite rendre \(30\) euros, la méthode gloutonne proposera \(6\) pièces (\(25+1+1+1+1+1\)) alors que la solution optimale n’en compte que \(3\) (\(10+10+10\)).

Comment résoudre ce problème avec la programmation dynamique ?

Tout d’abord il s’agit bien d’un problème d’optimisation.

Le cas le plus simple est lorsqu’il n’y a qu’un seul type de pièces, de \(1\) euro donc. On rend alors \(n\) pièces de \(1\).

Ensuite, si la pièce la plus grande (\(d_k\)) vaut plus que la somme à rendre, on peut sans problème considérer le sous problème consistant à rendre la même somme sans cette pièce : on a un sous-problème optimal.

Dernier cas de figure à gérer (le plus courant) : la somme à rendre \(n\) est plus grande que la plus grande valeur \(d_k\). De deux choses l’une :

• soit la solution optimale (que l’on cherche à déterminer) contient une pièce de cette valeur et dans ce cas on peut résoudre le problème comportant les mêmes pièces mais cherchant à rendre \(n-d_k\) (on a fait l’hypothèse que l’on rendait une pièce de valeur \(d_k\))
• soit la solution optimale ne contient pas cette pièce et dans ce cas il faut résoudre le problème contenant les pièces allant de \(d_1\) à \(d_{k-1}\) et cherchant toujours à rendre \(n\) euros

Il est impossible a priori de savoir quelle sera la solution optimale (celle avec \(d_k\) ou sans…) : il faut donc tester les deux hypothèses et à la fin retenir le meilleure (celle qui rend la somme souhaitée en un minimum de pièces).

La relation de récurrence liant les problèmes entre eux est alors :

\[Rendu(n \mbox{ euros}, k\mbox{ valeurs})\left\{ \begin{array}{lll} n & \mbox{si } k=1 \\ Rendu(n, k-1) & \mbox{si } k>1, d_k>n \\ min(Rendu(n, k-1),Rendu(n-d_k, k)+1) & \mbox{si } k>1, n>d_k \\ \end{array} \right. \]

Mettons que l’on souhaite déterminer le nombre de pièces minimal de pièces permettant de rendre \(n\) euros en utilisant le \(k\) pièces à notre disposition. On peut utiliser l’algorithme suivant :

Rendu_récursif(n, k) :
  Si k est égal à 1 :
    Retourner n # On rend n pièces de 1 centimes
  Sinon si la valeur de la k-ième pièces est strictement supérieure à n :
    Retourner Rendu_récursif(n, k-1) # La plus grande pièce est trop importante
  Sinon :
    # La plus grande pièce convient. On gère deux cas
    # 1er cas : on l'ignore
    sans_piece prend la valeur Rendu_récursif(n, k-1)
    # 2nd cas : on fait le rendu avec une de ces pièces      
    avec_piece prend la valeur Rendu_récursif(n - d_k, k) + 1
    # On garde le cas le plus intéressant
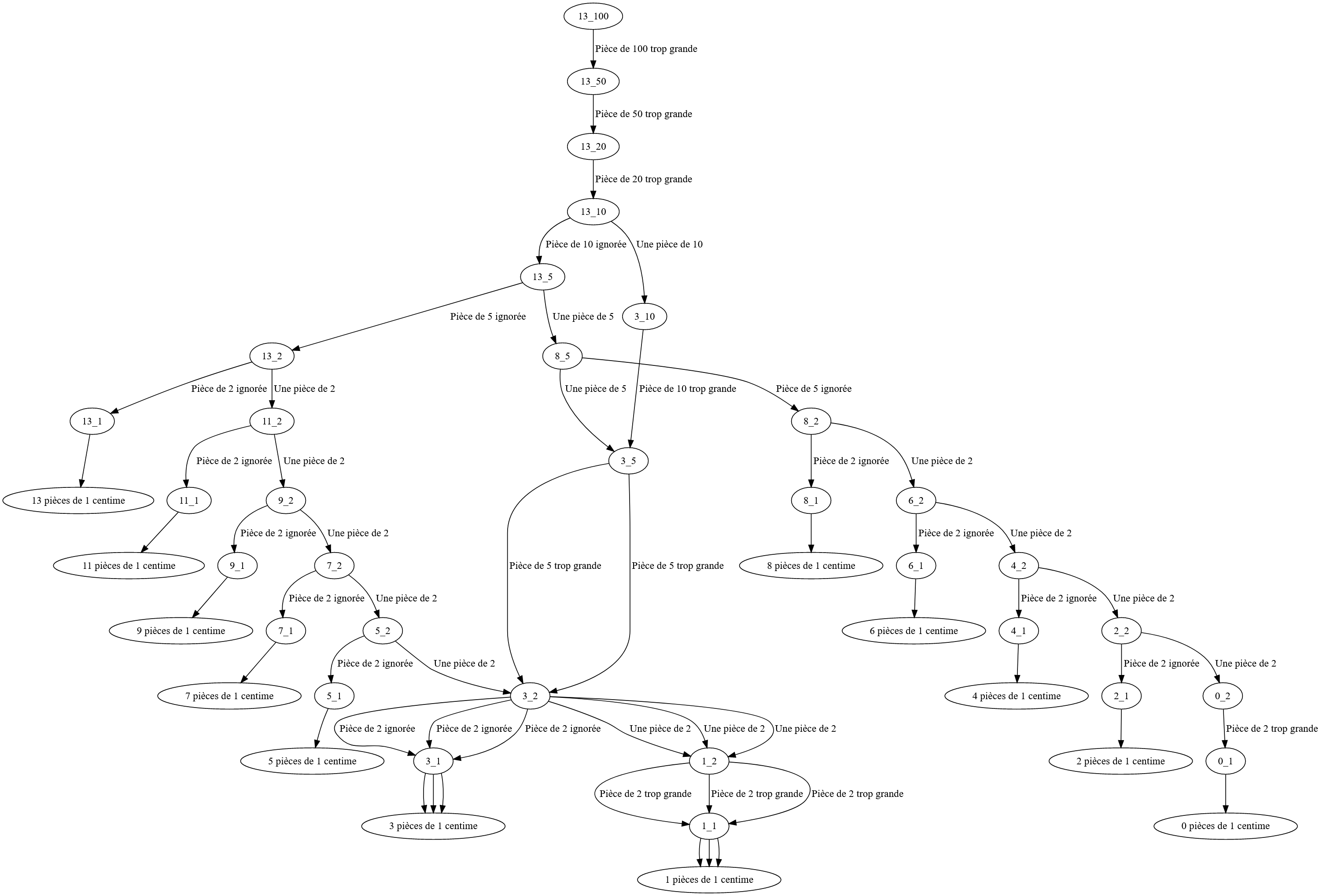
    Retourner le minimum de sans_piece et avec_piece

Si l’on utilise cet algorithme avec les pièces européennes (exprimées en centimes : \((1,2,5,10,20,50,100)\)) pour rendre \(13\) centimes, il propose le bon résultat : \(3\) pièces sont nécessaires. (\(10+2+1\)). Toutefois, comme dans l’exemple de la suite de Fibonacci, l’algorithme calcule plusieurs fois les mêmes valeurs comme on peut le voir sur la figure suivante présentant les appels récursifs (certains sommets sont appelés plusieurs fois).

Comme pour le calcul des termes de la suite de Fibonacci, la programmation dynamique prend ici son sens : on va garder trace des valeurs précalculées dans un tableau de \(n+1\) lignes (de \(0\) à \(n\) centimes) et \(k\) colonnes (une par pièce). Voici l’algorithme :

Rendu_dynamique(n, k, memoire = Null) :
  # On commence par créer la mémoire
  Si memoire vaut Null :
    memoire est une liste vide
    Pour i allant de 0 à n+1 :
      memoire[i] est une liste
      Pour j allant de 0 à k - 1 :
        memoire[i][j] vaut -1 # on initialise avec une valeur absurde
  
  Si memoire[n][k] est différent de -1 :
    # la valeur cherchée a déjà été calculée, on la retourne
    Retourner memoire[n][k]
  
  Si k est égal à 0 :
    # On rend n pièces de 1 centime
    memoire[n][k] prend la valeur de n
    Retourner n
  
  Sinon si pieces[k] > n :
    # La pièce en cours a une valeur supérieure à celle de la somme à rendre
    # On l'ignore
    memoire[n][k] prend la valeur de Rendu_dynamique(n,k-1, memoire)
    Retourner memoire[n][k]
  
  Sinon :
    # La pièce en cours est intéressante : deux cas de figure
    # 1er cas : on ne la prend pas
    cas_1 prend la valeur de Rendu_dynamique(n, k-1, memoire)
    # 2nd cas : on prend une pèce de cette valeur
    cas_2 prend la valeur de Rendu_dynamique(n - d_k, k, memoire)
    # On garde le minimum
    memoire[n][k] prend la valeur du minimum de cas_1 et cas_2
    Retourner memoire[n][k]

Cette méthode est plus efficace en termes de nombres de calculs (“seulement” 43 appels récursifs pour le rendu de \(13\) centimes). La figure présentant les appels récursifs est moins chargée

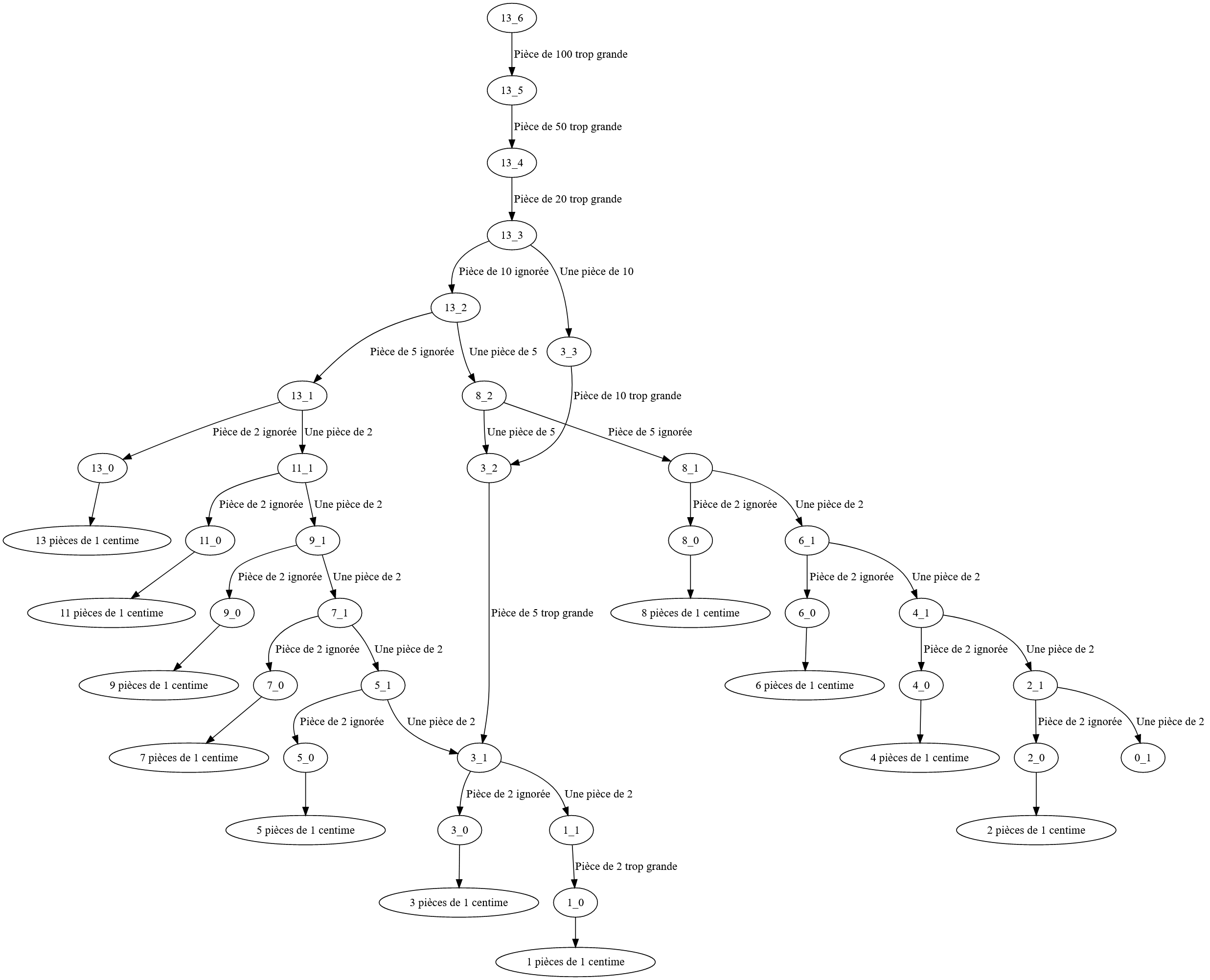
Cette méthode est-elle meilleur que la simple méthode récursive ? Comparons les calculs pour un rendu de \(2,27\) euros :

• Dans une approche bottom-up, en calculant toutes les valeurs intermédiaires, on calcule \(1\,824\) valeurs
• L’approche top-down récursive sans mémoisation fait \(263\,253\) appels à la fonction : certaines valeurs sont caclulées plusieurs fois…
• L’approche top-down avec mémoisation (la programmation dynamique donc) calcule 640 nombres ! On est meilleur que els deux méthodes précédentes