L’ADN des êtres vivants est constitué des bases l’adénine, la cytosine, la guanine et thymine que l’on abrège souvent en A, C, G et T. Le génome humain est ainsi constitué d’environ \(3\,400\) millions de paires de bases azotées : une chaîne de caractères de \(3\,400\) millions de lettres piochées dans l’alphabet {A,B,C,D} !

L’ADN permet de synthétiser les protéines constitutives des êtres vivants grâce à la correspondance \(3 \textrm{ bases azotées} = 1 \textrm{ acide aminé}\). Considérons une protéine de \(500\) acides aminés de long : son code génétique est une chaîne de \(1\,500\) bases. Comment chercher l’emplacement de ce code génétique au sein de l’ensemble du génome d’un humain ? Comment chercher efficacement un mot de \(1\,500\) lettres au sein d’un livre de \(3\,400\,000\,000\) de lettres ?

Afin de simplifier les choses, nous allons considérer l’exemple suivant : on se donne le texte “lundi je regarderai la lune avec la lunette” et l’on va chercher au sein de cette chaîne le motif “lunette”.

Le texte a une longueur de \(43\) caractères, le motif de \(7\). Chaque lettre d’une chaîne est indicée en partant de \(0\). Ainsi texte[1] est u.

I. Recherche naïve

L’approche naïve consiste à lire le texte du début à la fin en cherchant les correspondances avec le motif. Si la première lettre correspond, on essaie la deuxième, si elle correspond aussi, on passe à la troisième etc… Si les lettres ne correspondent pas, on décale le motif d’un rang et on recommence.

On obtient une correspondance pour le rang \(35\).

Voici l’algorihtme :

recherche_naive(motif, texte) :
  long_motif est la longueur du motif
  long_texte est la longueur du texte
  Pour rang allant de 0 à long_texte - long_motif :
    i = 0
    Tant que i est strictement inférieur à long_motif :
      Si texte[rang + i] est égal à motif[i] :
        i prend la valeur i + 1
      Sinon :
        Quitter le Tant que
    Si i est égal à long_motif :
      Afficher "Le motif apparaît au rang" rang

La boucle Pour principale ne va pas jusqu’à la fin du texte car il faut laisser de la place pour le motif (un motif de taille \(7\) ne tiendra pas sur les \(6\) derniers caractères !).

Pour chaque rang ensuite on teste successivement les correspondances entre la lettre du texte et celle du motif. S’il y a correspondance on passe à la lettre suivante, sinon, on quitte les tests et on passe au rang suivant. Si toutes les lettres correspondent, on affiche le rang en question.

Quelle est la complexité de cet algorithme ? Le pire des cas serait celui d’un texte comportant une répétition du motif : par exemple le texte “aaaaaaaaaa” (\(10\) a) dans lequel on cherche le motif “aa”. Dans ce cas, la boucle Pour va effectuer \(9\) itérations (\(10- 2 + 1\) car le motif ne peut pas débuter sur la dernière lettre du texte) et pour chacune testera \(2\) lettres. On aura donc \(9\times2 = 18\) itérations.

De façon générale, si la longueur du texte est \(n\) et celle du motif \(m\), la complexité est de \(O((n-m+1)\times m)\) (\(n-m+1\) est le nombre de positions possibles pour le motif dans le texte).

Dans le cas d’une recherche d’un motif de \(1\,500\) caractères dans un texte de \(3\,400\,000\,000\) de caractères cela fait \(5\,097\,751\,500\) itérations dans le pire des cas ! On doit pouvoir faire mieux…

Algorithme de Boyer-Moore

Cet algorithme a été développé par Robert S. Boyer et J. Strother Moore en 1977.

Le point de départ est plutôt contre-intuitif : pour chercher le motif dans le texte, on commence par la dernière lettre du motif ! En effet, si la lettre du texte correspondante n’est pas la bonne, il est inutile de tester les autres lettres. Cela ne change pas beaucoup par rapport à l’approche naïve.

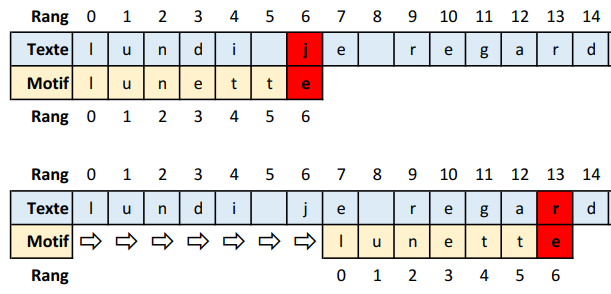
La vraie différence se situe dans l’action qui suit la comparaison des caractères:

Si la lettre observée ne fait même pas partie du motif, on peut alors décaler la fenêtre de lecture directement de la longueur du motif. On évite ainsi de faire autant de tests que le motif est long.

Que se passe-t-il lorsque la lettre du texte correspond à celle du motif ? On étudie alors les lettres précédentes jusqu’à avoir soit fini le motif (et donc trouvé une correspondance parfaite), soit trouvé un mauvais caractère.

Dernier cas de figure : le caractère lu n’est pas correct mais il apparaît toutefois à une autre position dans le motif. Dans ce cas on doit décaler la fenêtre de lecture afin de faire correspondre ce caractère et celui du motif situé le plus à droite (la dernière occurence de la lettre). C’est ce qui se passe entre les étapes 1 et 2 de la figure 4.

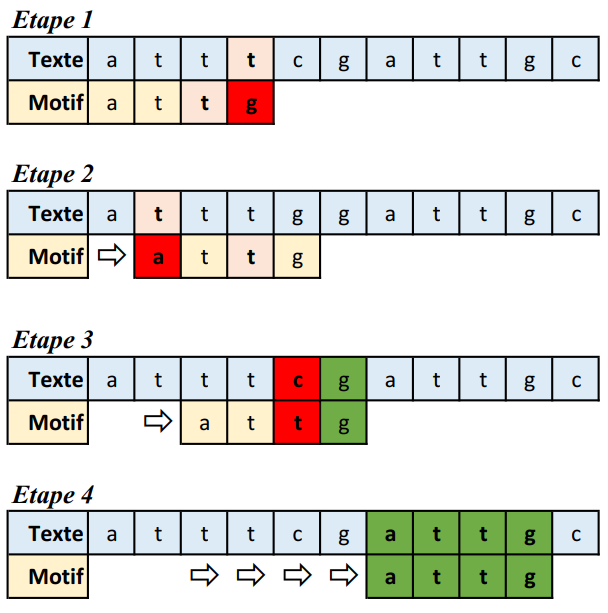
Il peut toutefois arriver que la dernière occurence du caractère cherché soit située plus loin dans le motif : le saut ferait alors reculer la fenêtre de lecture ce qui est inefficace. Dans ce cas, on se contente de faire un saut de \(1\) caractère. C’est ce qui se passe entre les étapes 2 et 3 de la figure 4.

L’algorithme de Boyer-Moore nécessite donc avant d’effectuer les comparaisons de savoir quels sont les décalages à effectuer. Pour ce faire il doit construire un dictionnaire decalages reprenant l’indice dans le motif de la dernière occurence de chacun de ses caractères.

La fonction suivante crée ce dictionnaire :

creation_decalage( motif) :
  # motif est le motif cherché
  
  dico est un dictionnaire vide
  long_motif est la longueur du motif

  Pour tous les caractère de motif :
    Ajouter une entrée caractère à dico
    dico[caractère] prend la valeur long_motif
    Pour i allant de 0 à long_motif - 1 :
      Si motif[long_motif - 1 - i] est égal à caractère :
        dico[caractère] prend la valeur i
        Sortir de la boucle Pour
  
  Renvoyer dico

On crée ici un dictionnaire dont les entrées sont les lettres du motif. On initialise chaque entrée avec un décalage égal à la longueur du motif. Ensuite on parcourt le motif de la droite vers la gauche et dès que l’on trouve le caractère en cours, on met à jour l’entrée correspondante du dictionnaire.

L’algorithme de Boyer-Moore peut alors être donné :

boyer_moore(texte, motif) :
  long_motif est la longueur du motif
  long_texte est la longueur du texte

  decalages prend la valeur creation_decalage(motif)

  occurences est un tableau vide

  position_texte = longueur_motif - 1
  # On commence par lire le dernier caractère du motif

  Tant que position_texte est strictement inférieur à long_texte :
    position_motif = 1
    # on débute par le dernier caractère du motif
    Tant que position_motif est strictement inférieur à longueur_motif + 1
    # Tant qu'il reste des caractères à tester dans le motif
      caractere prend la valeur de texte[position_texte - position_motif + 1]
      # On lit le caractère à tester
      
      Si motif[- position_motif] == caractere :
        # le caractère correspond, on passe au précédent
        position_motif += 1
      
      Sinon si le caractere est dans le motif :
        # le caractère est incorrect mais présent autrepart
        decalage prend la valeur de position_motif - decalages[caractere]
        position_texte augmente du maximum entre 1 et decalage
      
      Sinon :
        # le caractère n'apparaît pas dans le motif
        position_teste augmente de long_motif
        Sortir du Tant Que
      
      Si position_motif est égal à long_motif + 1 :
        # Tous les caractères correspondent
        Ajouter la valeur position_texte - longueur_motif + 1 à occurences
        Sortir du Tant Que
    
  Renvoyer occurences

L’analyse précise de la complexité de cet algorithme est trop technique. Il est toutefois intéressant de noter que, du fait des nombreux sauts, cette méthode de recherche ne lit pas le texte en entier. On peut même montrer qu’elle lit en moyenne une fraction \(\frac{\textrm{longueur du texte}}{\textrm{longueur du motif}}\) du texte. Ainsi, si la clé fait \(10\) caractères de long, l’algorithme lira en moyenne \(1\) caractère sur \(10\). On est loin des nombreuses lectures de la recherche naïve !

En vérité, l’algorithme de Boyer-Moore utilise aussi une autre façon de gérer les décalages mais cette seconde approche est trop technique pour ce cours et ne sera pas abordée.