- Architectures Matérielles -
Protocoles De Routage
Internet est grand ! En août 2020, Google référence plus de \(55\) milliards de pages web…
Ces pages sont enregistrées sur des millions de serveurs. Lorsqu’un utilisateur souhaite consulter une page, une requête parcourt le web jusqu’au serveur et celui-ci renvoie les données demandées.
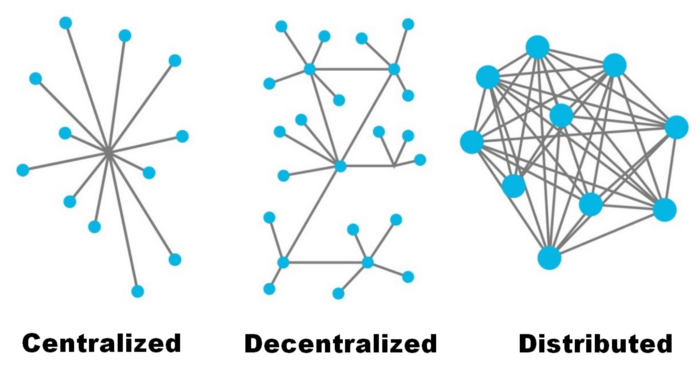
Bien sûr il n’existe pas un câble unique entre chaque utilisateur d’internet (relier \(n\) utilisateurs nécessiteraient alors \(\frac{n(n-1)}{2}\) câbles !). Le réseau est construit de façon décentralisée, distribuée. Cette structure est plus efficace (en particulier dans le cas de la panne d’un routeur) mais complique l’acheminement d’un paquet entre deux postes : quelle route choisir lorsque personne ne connaît l’ensemble de la carte du réseau ?

Le réseau internet peut être modélisé comme un graphe pondéré :
On pourrait encore affiner la description en considérant que le graphe est orienté (la liaison \(A \rightarrow B\) diffère de \(B \rightarrow A\)) mais ce n’est pas nécessaire dans le cadre de ce cours.
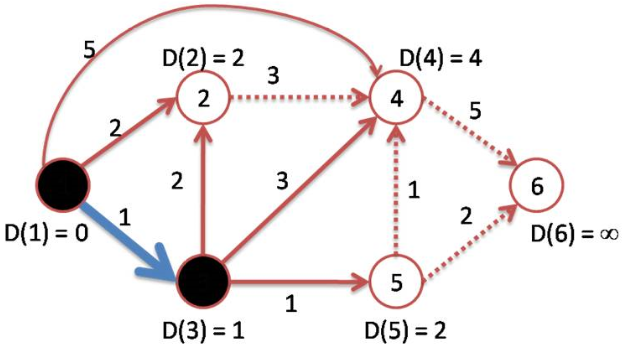
Considérons le graphe suivant de la figure 2. Les arcs sont orientés mais nous n’en tiendrons pas compte.
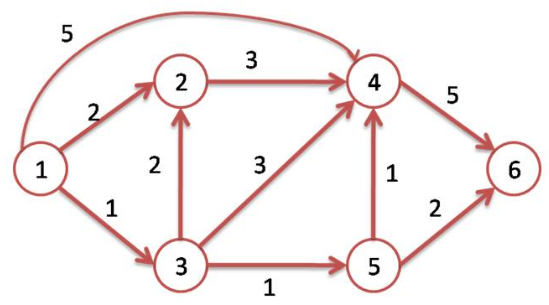
On souhaite déterminer le plus court chemin entre les sommets \(1\) et \(6\). L’algorithme classique utilisé sur le graphe dans ce cas de figure est l’algorithme de Dijkstra. L’idée est de parcourir tout le graphe à partir du sommet de départ en faisant en sorte que chaque sommet soit associé à son prédécesseur dans le plus court chemin le reliant à l’origine.
Concrètement, on commence par donner des poids à tous les sommets :
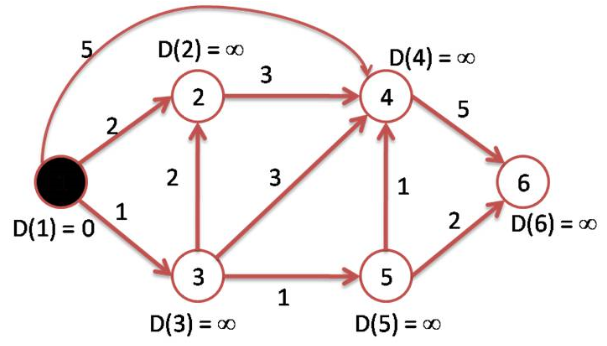
Ensuite, tant que l’on n’a pas visité tous les sommets du graphe on procède aux étapes suivantes :
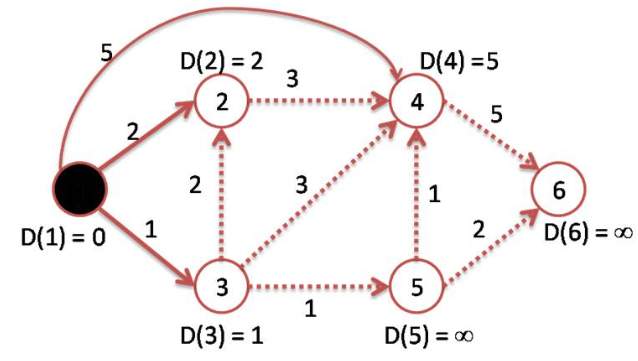
éventuellement on recalcule le poids des sommets déjà visités : si le dernier sommet étudié est voisin d’un sommet déjà visité et que le nouveau chemin d’accès est plus court que celui déjà calculé, on le met à jour (voir figure 5)
on choisit le sommet non visité ayant le plus petit poids (en cas d’égalité on choisit aléatoirement). On l’ajoute à la liste des visités et on lui associe le nom du sommet précédent
Lorsque tous les sommets ont été visités, on peut reconstruire le plus court chemin entre le sommet de départ et n’importe quel sommet en partant de l’arrivé et en “remontant” à l’orgine à l’aide des données des sommets précédents.
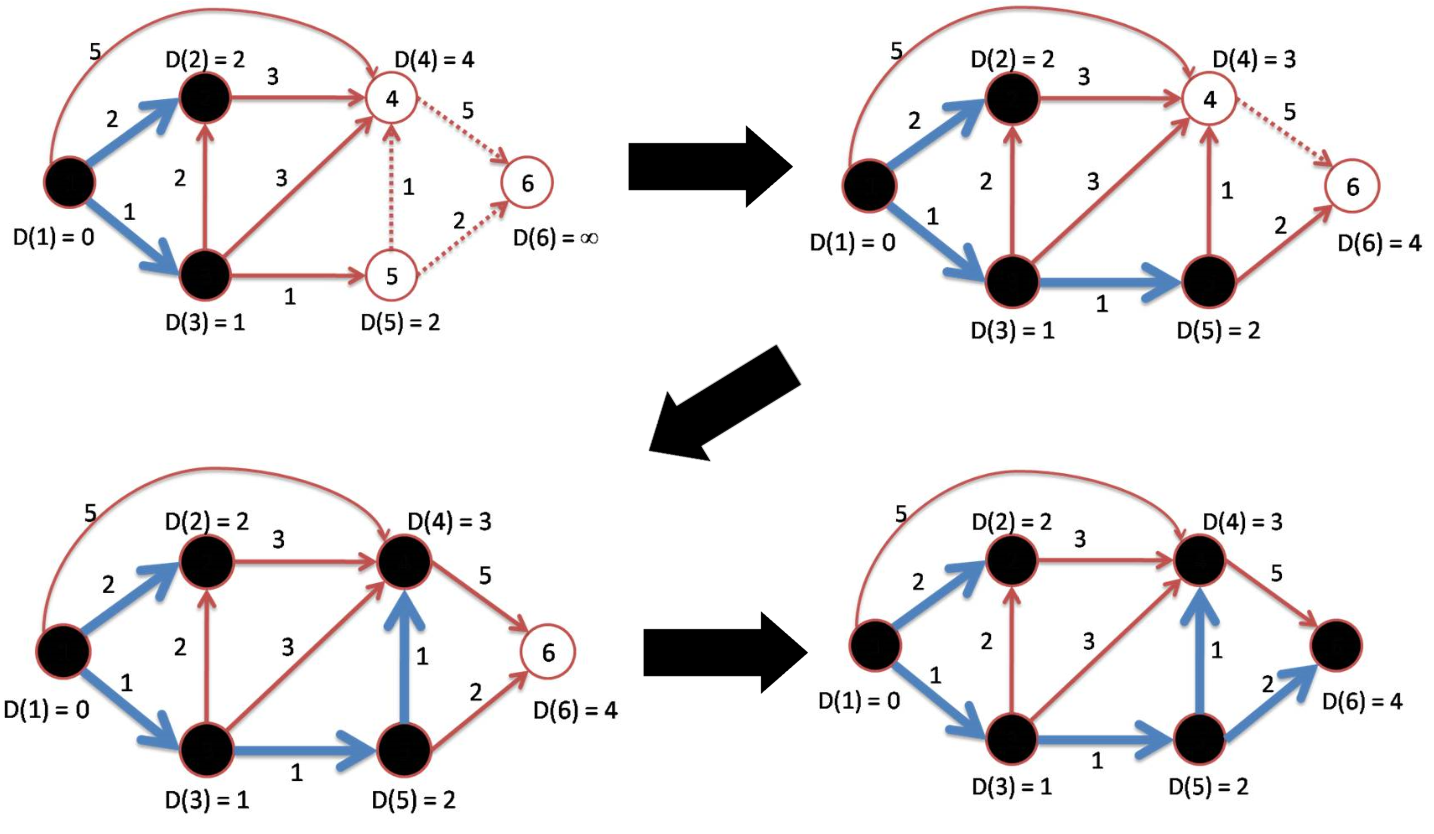
Dans le cas qui nous occupe, les étapes suivantes de l’algorithme sont représentées sur la figure 6.
A la fin du parcours, les sommets sont associés aux valeurs listées dans le tableau .
| Sommet | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Poids | 0 | 2 | 1 | 3 | 2 | 4 |
| Précédent | / | 1 | 1 | 5 | 3 | 5 |
Le chemin le plus court du sommet \(1\) au \(6\) est donc \(1 \rightarrow 3 \rightarrow 5 \rightarrow 6\) (on part de la colonne \(6\) et on remonte les prédecesseurs). Sa longueur est de \(4\).
Cet algorithme est optimal : il fournit toujours l’un des plus courts chemins (il peut en exister plusieurs). Pour un graphe comportant \(n\) sommets et \(a\) arcs, sa complexité est de \(O(a+nlog(n))\).
Il présente toutefois un très grand défaut dans le cadre d’internet : il faut en effet connaître l’ensemble du graphe afin de déterminer le meilleur chemin. Sur un réseau tel qu’internet c’est une condition irréalisable…
Dès l’orgine du réseau ARPAnet, d’autres méthodes de routage ont été utilisées. L’une d’entre elles est le protocole Routing information Protocol qui s’appuie lui-même sur l’algorithme de Bellman-Ford. Ces algorithmes utilisent une technique à vecteur de distance.
L’intérêt de ce protocole est que les sommets interagissent de façon individuelle et n’ont pas besoin de connaître l’ensemble du réseau (sa carte complète) afin de router les paquets selon le meilleur chemin.
L’un des points importants de ce protocole est d’utiliser le nombre de sauts comme métrique pour mesurer la longueur d’un chemin. Ainsi, si le chemin allant de \(A\) à \(C\) est \(A \rightarrow B \rightarrow C\) alors \(C\) est à \(2\) sauts de \(A\).
L’idée est la suivante :
chaque routeur du réseau a constamment en mémoire une table de routage. Celle-ci comprend une ligne par routeur du réseau et lui associe le nombre minimal de sauts pour l’atteindre et le nom du premier routeur de cette route
à intervalles réguliers (initialement toutes les \(30\) secondes) un routeur envoie une requête à tous les autres routeurs du réseau
les voisins directs du routeur lui répondent en lui envoyant leur table de routage
le routeur peut alors comparer ces réponses et sa table
Cette dernière comparaison est assez simple : si le routeur \(A\) reçoît de \(B\) une table lui indiquant que ce dernier peut joindre \(C\) en \(3\) sauts, alors \(A\) peut en déduire que \(C\) est à \(4\) sauts de lui (\(1\) pour aller en \(B\) puis \(3\) de \(B\) à \(C\)). Si la table de routage de \(A\) comprenait un chemin en \(5\) sauts ou plus vers \(C\), le routeur peut la mettre à jour en indiquant que désormais le meilleur chemin vers \(C\) fait \(4\) sauts de long et passe par \(B\).
Outre sa simplicité, ce protocole a l’avantage de converger (de tendre) vers une solution optimale. Il réagit très rapidement aux “bonnes nouvelles” (l’existence d’un nouveau chemin très court se propage très rapidement le long du réseau). Par contre, si un routeur tombe en panne, cette information met beaucoup de temps à être diffusée et peut même, à long terme, engendrer des chemins de taille infinie dans les tables ! Pour cette raison, l’algorithme RIP est limité au chemins de taille inférieures à \(16\) sauts ce qui restreint son utilisation à certains “petits” réseaux.
Le protocole Open Shortest Path First (OSPF) date des années 1990 et a été développé afin de pallier aux faiblesses des RIP en particulier sa faible adaptation aux réseaux des grande taille.
Il fait partie des protocoles par état de lien.
Régulièrement les routeurs du réseau envoient la liste de leurs voisins ainsi que le coût de la liaison correspondante. Ce coût est inversement proporitonnel au débit (en bits par secondes) de la ligne (plus le débit est important, plus le coût est faible).
Lorsqu’un routeur reçoit un tel message, il le transmet lui aussi à ses voisins : on parle de diffusion par inondation. Totuefois, afin d’éviter que ces messages ne circulent infiniment sur le réseau (en étant relayés encore et encore), ils sont accompagnés de données sur l’âge des informations. Lorsque l’âge est trop grand, le message est ignoré et non relayé.
Une fois qu’il a reçu les informations de nombreux routeurs, un poste peut construire la carte complète du réseau. Il aura alors la possibilité de faire fonctionner un algorithme de “plus court chemin” afin de déterminer les routes à utiliser.
Chaque routeur contient donc l’ensemble de la carte du réseau… A l’échelle d’internet c’est impossible. C’est pourquoi OSPF fonctionne à l’échelle de systèmes autonomes. Un système autonome peut par exemple être le réseau géré par une université ou l’ensemble des routeurs administrés par un fournisseur d’accès. Il en existe près de \(100\,000\) à l’échelle du globe !
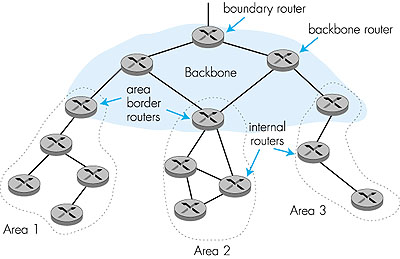
Un système autonome est construit autour d’une épine dorsale (backbone en anglais). Celle-ci permet de mettre en relation différentes zones (area en agnlais). On peut alors distinguer différents types de routeurs selon qu’ils sont intérieurs (de l’épine dorsale ou d’une zone) ou à l’interface entre elles.
Ces routeurs de frontières ont un statut particulier car ils doivent connaître l’ensemble des informations des deux espaces auxquels ils appartiennent (épine dorsale et zone). Les routeurs internes eux ne connaissent que les informations concernant leur espace propre.
Lorsqu’un message est adressé à l’intérieur d’une zone, le routage est direct. Si le destinataire est par contre situé dans une autre zone, le routage se fait en trois temps :
Et si le message est destiné à un poste situé hors du système autonome ? Il est alors acheminé à un routeur de frontière d’épine dorsale et transmis à un autre protocole qui aura pour tâche de l’acheminer au bon système autonome. Le plus utilisé actuellement est Border Gateway Protocol (BGP) qui recense plus de \(500\,000\) routes reliant des systèmes autonomes (notons au passage que ce nombre est si important que d’anciens routeurs n’ont pas la mémoire suffisante pour sauvegarder la table de routage et deviennent dès lors dysfocntionnels).
Il est possible de consulter les tables de routages de notre poste en utilisant les commandes suivantes :
netstat -rnGet-NetRoute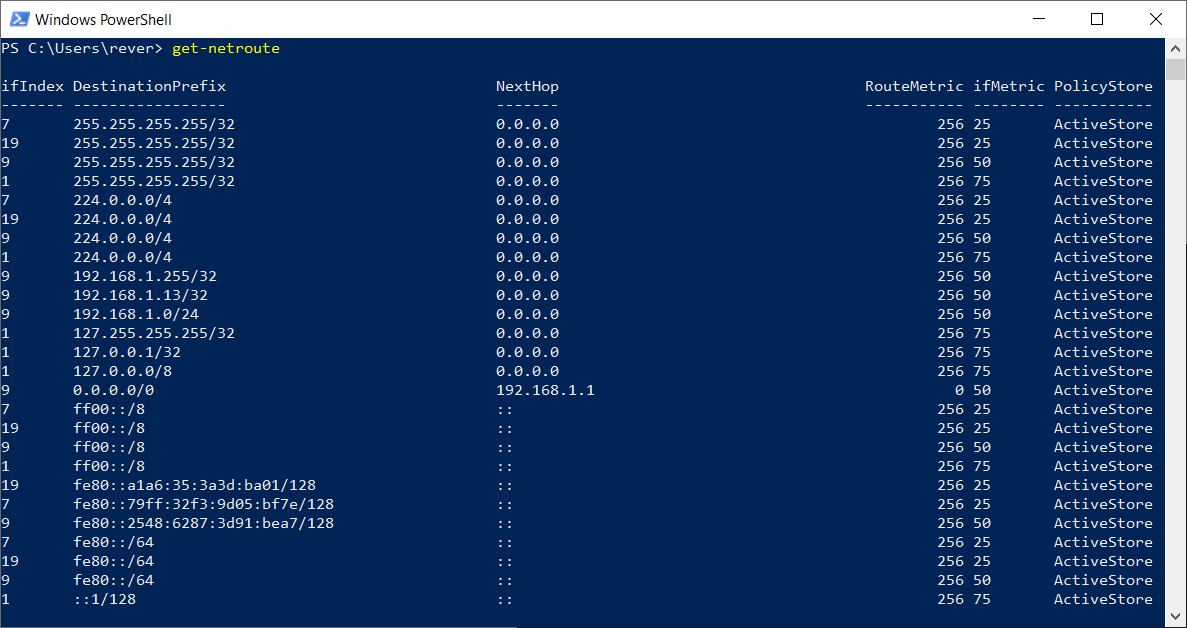
Comme on peut le voir sur la figure 8, les destinations sont affichées sous la forme 192.168.1.0/24.
Cette façon de faire désigne un sous-réseau.
Une adresse IP en version 4 est, nous l’avons vu en 1ère, composée de \(32\) bits (la version 6, en cours de mise en place, utilise \(128\) bits). Cette nomenclature permet de manipuler \(2^{32} =4\,294\,967\,296\), ce qui est beaucoup trop peu face à la multiplication des terminaux connectés à internet… Il a donc fallu trouver une astuce.
L’idée est de donner la même adresse à des terminaux différents mais en distinguant le réseau auquel ils
appartiennent. Une adresse réseau est ainsi fournie sous la forme X.X.X.X/bits où X.X.X.X
est une adresse IP classique et bits indique le nombre de bits (en partant de la gauche) qui
identifient le réseau.
Le routeur, à l’interface entre réseau privé et réseau public (internet), possède une adresse privée (celle du
réseau) et une adresse publique. Autant l’adresse privée peut être identique entre deux sous-réseaux (il y a fort à
parier que votre box a la même IP 192.168.1.1 privée que celle de votre voisin), autant les adresses
publiques sont obligatoirement différentes sans quoi les messages n’arriveraient pas au bon destinataire.
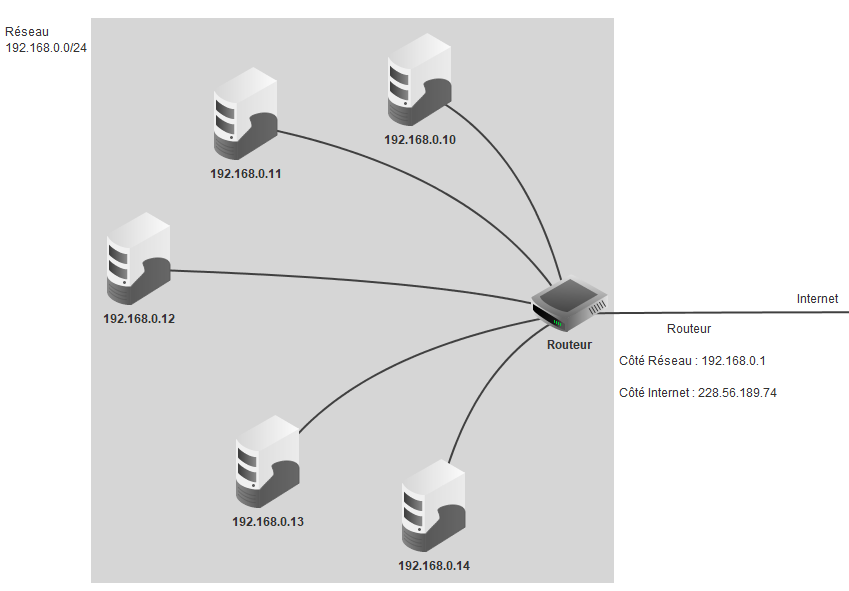
Ainsi, l’adresse 192.168.1.0/24 identifie le réseau par les \(24\)
premiers bits ce qui en laisse \(8\) pour nommer les machines au sein du réseau.
Comme \(2^8=256\), on peut utiliser cette adresse de réseau pour les structures de
petite taille (moins de \(256\) postes).
Lorsqu’une machine envoie un message, le destinataire est identifié par son adresse IP. Afin de savoir s’il fait
partie du même réseau que l’émetteur, on effectue l’opération binaire IP_dest AND IP_réseau. On peut
ainsi comparer bit par bit les deux adresses. Si le résultat est égal à l’IP_réseau alors le message
peut être acheminé en local.
Il existe trois plages d’IP réservées permettant de gérer des réseaux de tailles différentes.
| Adresse | Bits réseau | Bits machine | Nombre de machines possibles |
|---|---|---|---|
10.0.0.0/8 |
8 | 24 | \(2^{24} = 16\,777\,216\) |
172.16.0.0/12 |
12 | 20 | \(2^{20} = 1\,048\,576\) |
192.168.0.0/16 |
16 | 16 | \(2^{16} = 65\,536\) |
Les réseaux domestiques utilisent courament la dernière plage d’adresses : les IP des machines varient alors entre
192.168.0.1 et 192.168.255.254 (on réserve les adresses avec que des bits à 0
ou à 1 à des usages particuliers).