
- Architectures Matérielles -
Cryptographie
De tout temps, les hommes ont eu des secrets. Partager un secret est compliqué : on souhaite le dire à un proche mais sans que les autres ne l’entendent…
Pendant longtemps, le partage d’information a reposé sur des contraintes physiques : si personne ne m’entend dire le secret il n’y a pas de problème. Plus tard on a inventé les première méthodes de cryptage (du grec kryptos, caché). On parle aussi de méthodes de chiffrement. Pas sûr que César ait réellement utilisé le chiffre de César… Les techniques évoluant, certaines méthodes “simples” se sont avérées efficaces pendant longtemps. Le chiffre de Vigenère a ainsi tenu pendant trois siècles !
L’arrivée récente des ordinateurs a bousculé la donne : il est très facile désormais de crypter des messages mais il est aussi très simple de lancer une attaque force brute sur un message en testant toutes les clés possibles… Pourtant les besoins de sécurité des données ont augmenté : outre le caractère sensible de certaines informations (coordonnées bancaires…), la numérisation de la société a exposé une grande part de la vie personnelle de chacun. Aujourd’hui le moindre smartphone permet de stocker les photos personnelles du propriétaire, d’enregistrer les pages web qu’il visite voir même de suivre ses données médicales. Et tout cela est stocké en ligne dans le cloud. Dès lors il est indispensable que ces informations soient bien chiffrées.

Alice veut faire passer une information à Bob. Que cette information soit du texte, une image, un son, il est possible de la numériser et donc de l’écrire sous forme binaire. Par exemple le message Salut Bob s’écrit en binaire 01010011 01100001 01101100 01110101 01110100 00100000 01000010 01101111 01100010 grâce au code ASCII.
Les méthodes de cryptographie les plus simples sont dites symétriques : la clé utilisée pour chiffrer le message est la même que celle utilisée pour le déchiffrer.
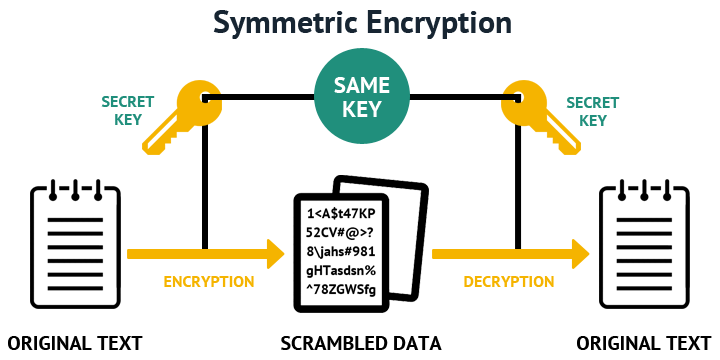
On connaît le chiffre de César, ou “A vaut K” : on décale chaque lettre d’un certain rang dans l’alphabet. La longueur du décalage est la clé. Si jamais on sort de l’alphabet, il suffit de boucler (la lettre qui suit Z devient A). Pour déchiffrer, on utilise la même clé mais on décale dans l’autre sens.
Il s’agit d’un chiffre par transposition : on se contente de remplacer une lettre par une autre. La version moderne travaille sur les bits. Partant par exemple d’un octet, on peut mélanger l’ordre des bits.
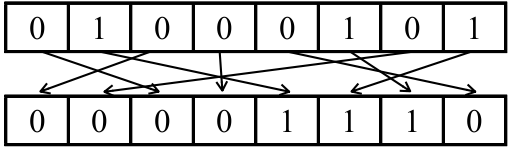
Dans la figure 3, si l’on numérote de \(0\) à \(7\) les bits selon leur poids (\(0\) est le bit de droite, de poids faible) alors la permutation transforme \(76543210\) en \(51746023\). Ce dernier nombre est la clé de chiffrement. Connaissant celle-ci, on trouve facilement la clé de déchiffrement : elle ramènerait le bit de poids faible en position \(3\), le suivant en position \(2\)…
Une autre méthode consiste à utiliser l’opérateur booléen XOR :
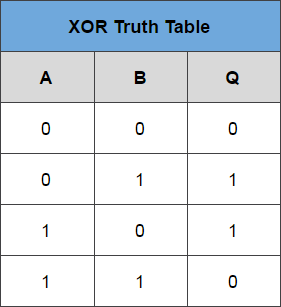
XORComme on peut le voir dans la table de vérité, cet opérateur renvoie \(1\) si les bits comparés sont différents, \(0\) dans le cas contraire.
Le cryptage consiste alors en l’application de la fonction XOR entre le nombre en clair et une clé (un nombre entier). Si la clé est par exemple \(89\), \(01011001_2\) en binaire, et que l’on souhaite crypter le nombre \(100\), \(01100100_2\), on fait \(100\) XOR \(89\) et l’on obtient \(61 = 00111101_2\).
L’un des avantage du XOR dans la cryptographie est que faire à nouveau un XOR avec la même clé sur le résultat crypté renvoie directement le nombre en clair : \(100\) XOR \(89 = 61\) mais aussi \(61\) XOR \(89 = 100\) ! La clé est vraiment symétrique.
Ces deux méthodes sont faciles à comprendre et à casser mais elles restent efficaces lorsqu’on les combine entre elles. Ainsi l’algorithme Advance Encryption Standart utilisé régulièrement de nos jours avec une clé de \(128\) bits et considéré comme sûr, utilise entre autres méthodes, des décalages de bits et des XOR. Aussi compliqué soit-il, il reste toutefois un algorithme de chiffrement symétrique.
Les méthodes de chiffrement symétrique, aussi subtiles et techniques soient-elles poseront toujours un problème : comment Alice peut-elle transmettre de façon sécurisée la clé à Bob ? Pour être sûre d’elle il faudrait crypter la clé. Mais dans ce cas il faut aussi transmettre la clé de cryptage permettant de crypter la clé… On ne s’en sort pas !
Une solution est apparue au milieu des années 1970 : le chiffrement asymétrique. On utilise alors des clés différentes pour crypter le message et le décrypter.

Dans les faits, avant de commencer à communiquer, Alice crée deux clés :
Intercepter la clé publique ne présente aucun intérêt : elle ne sert qu’à chiffrer.
La méthode la plus commune de chiffrement asymétrique utilisée aujourd’hui est RSA développée en 1977 par Ron Rivest, Adi Shamir, et Leonard Adleman. Basée sur des propriétés mathématiques assez abordables (niveau bac+2), sa sécurité repose sur la difficulté actuelle des ordinateurs à décomposer des nombres entiers en facteurs premiers. En effet, il est facile de calculer que \(1\,299\,709\times1\,159\,523=1\,507\,042\,478\,807\) (\(1\,299\,709\) et \(1\,159\,523\) sont des nombres premiers). Il est par contre beaucoup plus compliqué (à la main comme à l’aide d’un ordinateur) de décomposer \(1\,507\,042\,478\,807\) sous la forme \(1\,299\,709\times1\,159\,523\).

Ces méthodes de chiffrement asymétrique sont néanmoins assez lourdes à mettre en place en termes de calculs aussi les utilise-t-on surtout pour transmettre de façon sécurisée des clés associées à des chiffrements symétriques. Ceux-ci sont en effet moins gourmands en calculs. Une fois la clé transmise, on quitte les méthodes asymétriques.
Lorsque l’on visite une page sur le web, le trafic passe par de nombreux routeurs et peut alors être intercepté par des pirates. Ceux-ci peuvent par exemple filtrer les données échangées entre le client et le serveur afin de les lire ou d’en injecter de nouvelles : c’est une attaque Man In The Middle.
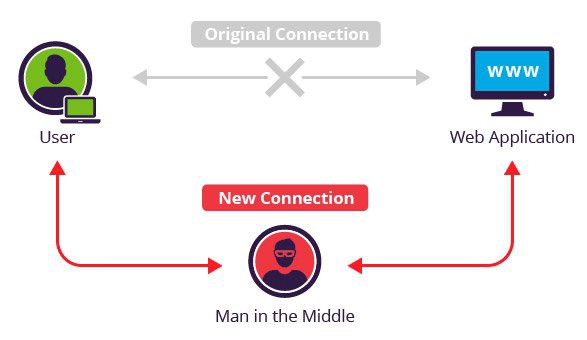
L’une des façons de se protéger de ce genre d’attaque est d’utiliser le protocle HTTPS. L’idée est la suivante :
